Математические чудеса и тайны

Мартин Гарднер

Перед вами обычная квадратная шахматная сетка из 64 клеток. На ваших глазах делается несколько разрезов и из получившихся частей составляется прямоугольник, в котором, однако, всего 63 клетки!

Вы задумали число — одно из тех, что написаны на карточках, разбросанных по столу. Ваш партнер поочередно трогает карточки указкой, а вы в это время произносите про себя по буквам задуманное число, и когда вы доходите до последней буквы, указка останавливается как раз на вашем числе!

Фокусы? Да, если хотите; а лучше сказать — эксперименты, основанные на математике, на свойствах фигур и чисел и лишь облеченные в несколько экстравагантную форму. И понять суть того или иного эксперимента — это значит понять пусть небольшую, но точную математическую закономерность.

Вот этой скрытой математичностью и интересна книга Мартина Гарднера. Скрытой — потому что по большей части сам автор не формулирует на языке математики закономерностей, лежащих в основе его экспериментов, ограничиваясь описанием действий показывающего, явных и тайных; но читателю, знакомому с элементами школьной алгебры и геометрии, несомненно, доставит удовольствие самому восстановить по объяснениям автора соответствующую алгебраическую или геометрическую идею. Впрочем, в отдельных, более интересных случаях (отмеченных числами с круглой скобкой) мы позволили себе сопроводить изложение автора небольшими примечаниями, выявляющими математическую суть его построений, эти примечания помещены в конце книги.

Математические фокусы — очень своеобразная форма демонстрации математических закономерностей.

Если при учебном изложении стремятся к возможно большему раскрытию идеи, то здесь для достижения эффективности и занимательности, наоборот, как можно хитрее маскируют суть дела. Именно поэтому вместо отвлеченных чисел так часто используются различные предметы или наборы предметов, связанные с числами: домино, спички, часы, календарь, монеты и даже карты (разумеется, такое использование карт не имеет ничего общего с бессмысленным времяпровождением азартных игроков; как указывает автор, здесь карты рассматриваются тросто как одинаковые предметы, которые удобно считать; имеющиеся на них изображения не играют при этом никакой роли).

Мы надеемся, что книга Гарднера будет интересна многим читателям: юным участникам иисольных математических кружков, взрослым «неорганизованным» любителям математики, а может быть, тот или иной из описанных здесь экспериментов пробудит улыбку и у серьезного ученого в краткий момент отдыха от большой работы.

Г. Е. Шилов

Подобно многим другим предметам, находящимся на стыке двух дисциплин, математические фокусы не пользуются особым вниманием ни у математиков, ни у фокусников. Первые склонны рассматривать их как пустую забаву, вторые пренебрегают ими как слишком скучным делом. Математические фокусы, скажем прямо, не принадлежат к той категории фокусов, которая может держать зачарованной аудиторию из неискушенных в математике зрителей; такие фокусы обычно отнимают много времени, и они не слишком эффектны; с другой стороны, вряд ли найдется человек, собирающийся черпать глубокие математические истины из их созерцания.

И все-таки математические фокусы, подобно шахматам, имеют свою особую прелесть. В шахматах объединено изящество математических построений с удовольствием, которое может доставить игра. В математических же фокусах изящество математических построений соединяется с занимательностью. Неудивительно поэтому, что наибольшее наслаждение они приносят тому, кто одновременно знаком с обеими этими областями.

Настоящая книга, насколько мне известно, представляет собой первую попытку обзора всей области современного математического фокуса. Большая часть материала книги взята из специальной литературы посвященной фокусам, а не из развлекательной математической литературы. По этой причине лица, изучавшие развлекательную математическую литературу, но незнакомые с современной специальной литературой, посвященной фокусам, вероятно, встретят в этой книге новую область развлекательного знания — новое богатое поле, о существовании которого они могли совершенно не подозревать.

Нью-Йорк, 1955 г.

---

Игральные карты обладают некоторыми специфическими свойствами, которые можно использовать при составлении фокусов математического характера. Мы укажем пять таких свойств.

1. Карты можно рассматривать просто как одинаковые предметы, которые удобно считать; имеющиеся на них изображения не играют при этом никакой роли.

С таким же успехом можно было бы пользоваться камешками, спичками или листочками бумаги.

2. Картам можно приписывать числовые значения от 1 до 13 в зависимости от того, что изображено на их лицевой стороне (при этом валет, дама и король принимаются соответственно за 11, 12 и 13) [1]).

3. Их можно делить на четыре масти или на чёрные и красные карты.

4. Каждая карта имеет лицевую и обратную стороны.

5. Карты компактны и одинаковы по размеру. Это позволяет раскладывать их различным образом, группируя в ряды или составляя кучки, которые тут же можно легко расстроить, просто смешав карты.

Благодаря такому обилию возможностей карточные фокусы должны были появиться очень давно, и можно считать, что математические фокусы с картами, безусловно, столь же стары, как сама игра в карты.

По-видимому, наиболее раннее обсуждение карточных фокусов, выполненное математиком, встречается в развлекательной книжке Клода, Гаспара Баше (Claud Gaspard Bachet «Problemes plaisants et delectables»), вышедшей во Франции в 1612 году. Впоследствии упоминания о карточных фокусах появлялись во многих книжках, посвященных математическим развлечениям.

Первым и, возможно, единственным философом, снизошедшим до рассмотрения карточных фокусов, был американец Чарлз Пейрс (Charles Peirce). В одной из своих статей он признается, что в 1860 году «состряпал» несколько необыкновенных карточных фокусов, основанных, пользуясь его терминологией, на «циклической арифметике». Два таких фокуса он подробно описывает под названием «первый курьез» и «второй курьез».

«Первый курьез» основан на теореме Ферма. Для одного лишь описания способа его демонстрации потребовалось 13 страниц н дополнительно 52 страницы были заняты объяснением его сущности. И хотя Пейрс сообщает о «неизменном интересе и изумлении публики», вызываемом его фокусом, кульминационный эффект этого фокуса представляется настолько не соответствующим сложности приготовлений, что трудно поверить, что зрители не погружались в сон задолго до окончания его демонстрации.

Вот пример того, как в результате видоизменения способа демонстрации одного старого фокуса необычайно возросла его занимательность.

Шестнадцать карт раскладываются на столе лицевой стороной кверху в виде квадрата по четыре карты в ряд. Кому-нибудь предлагается задумать одну карту и сообщить показывающему, в каком вертикальном ряду она лежит. Затем карты собираются правой рукой по вертикальным рядам и последовательно складываются в левую руку. После этого карты снова раскладываются в виде квадрата последовательно по горизонталям; таким образом, карты, лежавшие при первоначальной раскладке в одном и том же вертикальном ряду, теперь оказываются в одном к том же горизонтальном ряду. Показывающему нужно запомнить, в каком из них лежит теперь задуманная карта. Далее зрителя просят еще раз указать, в каком вертикальном ряду он видит свою карту, Понятно, что после этого показывающий может сразу же указать задуманную карту, которая будет лежать на пересечении только что названного вертикального ряда и горизонтального ряда, в котором, как известно, она должна находиться. Успех этого фокуса, конечно, зависит от того, следит ли зритель за процедурой настолько внимательно, чтобы распознать суть дела.

А теперь расскажем, как этот же самый принцип используется в другом случае.

Показывающий усаживается за стол вместе с четырьмя зрителями. Он сдает каждому (включая себя) по пяти карт, предлагает всем посмотреть их и одну задумать. Затем собирает карты, раскладывает их на столе в пять кучек и просит кого-нибудь указать ему одну из них. Далее берет эту кучку в руки, раскрывает карты веером, лицевой стороной к зрителям, и спрашивает, видит ли кто-нибудь из них задуманную карту. Если да, то показывающий (так и не заглянув ни разу в карты) сразу же ее вытаскивает. Эта процедура повторяется с каждой из кучек, пока все задуманные карты не будут обнаружены. В некоторых кучках задуманных карт может вовсе не оказаться, в других же их может быть две и более, но в любом случае карты отгадываются показывающим безошибочно.

Объясняется этот фокус просто. Пятерки карт нужно собирать начиная от первого зрителя, сидящего слева от вас, и далее по часовой стрелке (карты держат лицевой стороной книзу); карты показывающего будут при этом последними и окажутся сверху пачки. Затем все карты раскладываются в кучки по пяти карт в каждой. Любая из кучек может быть открыта зрителям.

Теперь, если задуманную карту видит зритель номер два, то эта карта будет второй, считая сверху кучки.

Если свою карту видит четвертый зритель, она будет четвертой в кучке. Иными словами, местоположение задуманной карты в кучке будет соответствовать номеру зрителя, считая слева направо вокруг стола (т, е. по часовой стрелке). Это правило имеет силу для любой кучки.

После небольшого размышления становится ясным, что в рассматриваемом фокусе, точно так же как и в предыдущем, применяется один и тот же принцип с пересечением рядов. Однако в последней варианте «пружинка» замаскирована гораздо лучше, благодаря чему получается значительно больший внешний эффект.

На ближайших страницах мы остановимся на тех фокусах, которые могут показаться более оригинальными или занимательными; при этом мы постараемся проиллюстрировать как можно больше математических принципов, на которых они могут быть основаны.

Здесь мы рассмотрим только те фокусы, в которых карты используются как однородные предметы независимо от того, что изображено на их лицевой стороне.

Собственно, здесь нам подошел бы любой набор небольших предметов, например камешков, спичек или монет, однако лучше всего воспользоваться все-таки картами, потому что их удобнее держать в руках и считать.

Показывающий просит кого-нибудь из зрителей снять небольшую пачку карт сверху колоды, после чего сам тоже снимает пачку, но с несколько большим количеством карт. Затем он пересчитывает свои карты.

Допустим, их двадцать. Тогда он заявляет: «У меня больше, чем у вас, на четыре карты и еще столько, чтобы досчитать до шестнадцати». Зритель считает свои карты. Допустим, их одиннадцать. Тогда показывающий выкладывает свои карты по одной на стол.

Считая при этом до одиннадцати. Затем в соответствии со сделанным им утверждением откладывает четыре карты в сторону и продолжает класть карты, считая далее; 12, 13, 14, 15, 16. Шестнадцатая карта будет последней, как он и предсказывал.

Фокус можно повторять снова и снова, причем число откладываемых в сторону карт нужно все время менять, например одни раз их может быть три, другой — пять и т. д. При этом кажется непонятным, как показывающий может угадать разницу в числе карт, не зная числа карт, взятых зрителем.

Объяснение. В этом тоже несложном фокусе показывающему совсем не нужно знать числа карт, имеющихся на руках у зрителя, но он должен быть уверенным, что взял карт больше, чем зритель. Показывающий считает свои карты; в нашем примере их двадцать. Затем произвольно берет какое-нибудь небольшое число, скажем четыре, и отнимает его от 20; получается 16. Затем показывающий говорит: «У меня больше, чем у вас, на четыре карты и еще столько, чтобы досчитать до шестнадцати». Карты пересчитываются, как это объяснялось выше, и утверждение оказывается справедливым [2]).

Колода карт тасуется зрителем. Показывающий кладет ее в карман и просит кого-либо из присутствующих назвать вслух любую карту. Предположим, что будет названа дама пик. Тогда он опускает руку в карман и достает какую-то карту пиковой масти; это, поясняет он, указывает масть названной карты. Затем он вытаскивает четверку и восьмерку, что дает в сумме 12 — числовое значение дамы.

Объяснение. Перед демонстрацией этого фокуса показывающий вынимает из колоды трефового туза, двойку черв, четверку пик и восьмерку бубен. Затем прячет эти карты в карман, запоминая их порядок.

Перетасованная зрителем колода тоже опускается в карман, причем так, чтобы отобранные четыре карты оказались сверху колоды. Присутствующие и не подозревают о том, что при тасовании колоды четыре карты уже были в кармане показывающего.

Числовые значения отложенных четырех карт образуют ряд чисел (1, 2, 4, 8), каждое из которых вдвое больше предыдущего, а в этом случае, как известно, можно, комбинируя их различными способами, получить в сумме любое целое число от 1 до 15.

Карта требуемой масти вытаскивается первой. Если она должна участвовать в комбинации карт, дающих в сумме нужное число, тогда ее включают в общий счет вместе с одной или несколькими картами, которые вытаскиваются из кармана дополнительно. В противном случае первая карта откладывается в сторону, а из кармана вынимается одна или несколько карт, необходимых для получения нужного числа.

При показе нашего фокуса случайно может быть названа и одна из четырех отобранных карт. В этом случае показывающий вытаскивает из кармана сразу ее — настоящее «волшебство»!

Встреченный нами в этом фокусе ряд чисел, из которых каждое последующее вдвое больше предыдущего, применяется и во многих других математических фокусах.

Кто-нибудь из зрителей тасует колоду карт и кладет ее на стол. Показывающий пишет название карты на листке бумаги и, не показывая никому написанного, переворачивает листок надписью вниз.

После этого на столе раскладываются 12 карт лицевой стороной вниз. Кого-нибудь из присутствующих просят указать четыре из них. Эти карты тут же открываются, а оставшиеся восемь карт собираются и кладутся под колоду.

Предположим, что были открыты тройка, шестерка, десятка и король. Показывающий говорит, что на каждую из этих четырех карт он будет укладывать карты из колоды до тех пор, пока не досчитает до десяти, начиная с числа, следующего за числовым значением данной карты. Так, например, на тройку придется положить семь карт, произнося при этом: «4, 5, 6, 7, 8, 9, 10»; на шестерку нужно будет уложить четыре карты; на десятку класть ничего не придется; фигурной карте в этом фокусе также приписывается числовое значение 10.

Затем числовые значения карт складываются:

3 + 6 + 10 + 10 = 29

Остаток колоды передается зрителю, и его просят отсчитать 29 карт. Последняя из них открывается. Листок с предсказанной заранее картой переворачивается, и написанное читается вслух. Конечно, там будет название только что открытой карты!

Объяснение. После того как колода будет перетасована, показывающий должен незаметно посмотреть, какая карта лежит внизу колоды. Именно эту карту он и предсказывает. Все остальное выходит само собой. После того как восемь из двенадцати карт будут собраны и положены под колоду, замеченная карта окажется по порядку сороковой. Если все операции, о которых говорилось выше, были выполнены правильно, мы неизменно будем приходить к этой карте [3]). То обстоятельство, что колода вначале тасуется, делает этот фокус особенно эффектным.

Интересно заметить, что в описанном фокусе, как и в других, основанных на том же принципе, показывающий может разрешить зрителю приписывать любые числовые значения валетам, дамам и королям.

Например, зритель может пожелать считать каждый валет тройкой, даму — семеркой, а короля — четверкой. Это никак не скажется на показе фокуса и может придать ему больше «таинственности».

Фокус, собственно, требует только одного: чтобы в колоде были 52 карты; какие это будут карты, не играет ни малейшей роли. Если все они будут двойками, фокус тоже получится. Это означает, что зритель может приписать любой карте новое значение, какое ему вздумается, причем это не повлияет на успех фокуса.

Несколько лет назад было предложено удивительное усовершенствование этого фокуса. Перетасовав колоду, показывающий выкладывает кучку в девять карт лицевой стороной вниз. Зритель выбирает одну из этих карт, запоминает ее и кладет на верх кучки.

Оставшаяся часть колоды кладется на кучку, и таким образом, замеченная карта оказывается девятой снизу.

Теперь показывающий берет катоду и начинает выкладывать карты по одной в кучку лицевой стороной кверху, считая при этом вслух в обратном порядке от 10 до 1. Если числовое значение положенной карты случайно совпадает с называемой цифрой (например, появилась четверка в то время, когда он произнес: «четыре»), то откладывание карт в эту кучку прекращается и начинается откладывание следующей кучки. Если же такого совпадения появляющейся карты и произносимого числа не произошло, то отсчитывание заканчивается на цифре 1 и кучка «бьется», т. е. накрывается следующей по порядку картой (лицевой стороной вниз), взятой сверху колоды.

Так выкладываются четыре кучки, после чего числовые значения «непобитых» (открытых) карт, лежащих сверху кучек, складываются. Отсчитав теперь из катоды это число карт, зритель обнаруживает под последней из них выбранную им карту. Этот вариант фокуса гораздо эффектнее прежнего, так как выбор карт, входящих в сумму, кажется совершенно случайным, а «принцип компенсации», на котором основан фокус, скрыт значительно глубже [4])

Многие диковинки из области теории чисел можно с успехом демонстрировать как карточные фокусы.

В качестве примера приведем следующий фокус. Он основан на том, что если умножить «циклическое число» 142857 на любое целое чисто от 2 до 6, то поручится число, составленное из тех же цифр с круговой (циклической) их перестановкой.

Фокус состоит в следующем. Зрителю даются пять карт красной масти, имеющие чистовые значения 2, 3, 4, 5 и 6. Себе же показывающий берет шесть карт черной масти, размещая их так, чтобы их числовые значения соответствовали цифрам числа 142857. Как показывающий, так и зритель тасуют свои карты; при этом показывающий только делает вид, что тасует, а в самом деле сохраняет и порядок неизменным.

(Этого можно легко добиться, дважды перекладывая карты по одной с одной стороны колоды на другую.

Быстрое выполнение этой операции создает полное впечатление тасовки, хотя весь эффект состоит в том, что расположение карт дважды меняется на обратное, оставляя таким образом первоначальный порядок неизменным.)

Показывающий раскладывает на столе карты в ряд, лицевой стороной кверху, образуя число 142857.

Зритель вытягивает одну из своих карт и кладет ее лицевой стороной вверх под рядом, разложенным показывающим. С помощью карандаша и бумаги зритель перемножает наше число на числовое значение вытянутой им карты. Пока он занят этим делом, показывающий собирает свои карты, накладывает на первую слева карту соседнюю, затем на нее соседнюю и т. д., «снимает» их один раз и снова кладет на стол кучкой (лицевой стороной книзу) [5]). После того как зритель выполнит умножение, показывающий берет свою кучку карт и снова раскладывает их слева направо лицевой стороной кверху. Шестизначное число, которое при этом получается, в точности совпадает с результатом умножения, найденным зрителем.

Объяснение. Карты черной масти показывающий собирает, не нарушая порядка, в котором они были разложены. Допустим, что зритель умножал наше число на 6: тогда произведение должно оканчиваться двойкой, так как шесть раз по семь (это последняя цифра множимого) будет сорок два. Если снять так, чтобы двойка оказалась внизу, то после того как карты будут разложены в ряд, она окажется последней картой и изображаемое картами число совпадет с ответом, полученным зрителем.

Циклическое число 142857 является обратным по отношению к простому числу 7 в том смысле, что оно получается от деления 1 на 7. Выполняя это деление, мы получаем бесконечную периодическую дробь с периодом, совпадающим с нашим циклическим числом.

Другие, большие, циклические числа также можно получить путем деления единицы на большие простые числа.

Пока показывающий стоит спиной к зрителям, кто-нибудь из них вынимает карту из колоды, кладет ее в карман и тасует колоду. Затем показывающий поворачивается, берет колоду и начинает выкладывать карты по одной лицевой стороной кверху. После того как выйдут все карты, он называет недостающую.

Объяснение. Числовое значение недостающей карты можно установить, подсчитав в уме сумму числовых значений карт, выложенных на стол. При этом валетам приписывают значение 11, дамам 12. Королей можно считать нулями и не учитывать вовсе.

Без королей сумма числовых значений всех карт в полной колоде равна 312. Поэтому, чтобы найти числовое значение отсутствующей карты, нужно из 312 отнять сумму числовых значений 51 карты. Если эта последняя сумма окажется равной 312, то недостающая карта — король.

При показе этого фокуса важно владеть методами быстрого счета. Так, например, очевидно, что, прибавляя 11, удобно сначала прибавить 10, а затем еще единицу, а для прибавления 12 вы сначала прибавляете 10, а затем двойку. Дальнейшею увеличения быстроты счета можно достичь путем «отбрасывания двадцаток», т. е. считая по модулю 20. Иначе говоря, как только сумма превзойдет 20, отбросьте это число и держите в памяти только остаток. После того как будет положена последняя карта, вам придется запомнить небольшое число от 0 до 12 включительно. Отнимите это число от 12, и вы получите числовое значение отсутствующей карты. Если последней суммой окажется 12, то недостающая карта — король. Нам кажется, что исключение «двадцаток» — лучший способ убыстрения счета. Однако многие предпочитают в этом случае отбрасывать 13. Тогда, например, складывая 7 и 8 и отбрасывая 1З, вы запоминаете 2. Вместо добавления 11 (в случае валета) и последующего отбрасывания 13 проще, ничего не добавляя, вычесть 2.

В случае дамы отбросьте 1. Ясно, что королей принимать во внимание не нужно. Закончив подсчет, отнимите последнюю цифру от 13 и вы получите числовое значение спрятанной карты. После того как оно найдено, можно, конечно, сдавая карты вторично, узнать масть отсутствующей карты. Однако при этом сразу раскрывается секрет фокуса. Как же определить масть карты при первой раскладке, одновременно с ее числовым значением?

Один из способов, — правда трудный, если вы не владеете техникой быстрого счета в уме, — это одновременное запоминание суммарного числа для масти и такого же числа для числового значения карты.

Припишем, например, картам пиковой масти числовое значение 1, трефовой — 2, червонной — 3, бубновой — нуль (и в расчет их не принимаем). При сложении отбрасываются десятки, и в итоге получается одно из четырех чисел: 5, 6, 7 или 8. Отнимая его от восьми, вы найдете масть спрятанной карты.

Вот другой метод прослеживания сумм числовых значений карт и числовых значений мастей. Установим какой-нибудь порядок мастей, скажем, пики, червы, трефы, бубны. Прежде чем открыть первую карту, скажем про себя: 0-0-0-0. Если первой картой окажется, например, семерка черв, произнесите про себя 0-7-0-0. Если следующей картой будет, скажем, пятерка бубен, счет изменяется на 0-7-0-5.

Другими словами, приходится держать в памяти изменяющуюся сумму по всем четырем мастям. Если из колоды изъята только одна карта, то при подсчете всех четырех изменяющихся сумм необходимо включать королей. Сумма чистовых значений карт для каждой из четырех мастей должна быть в этом случae равна 91. Но так как одна карта спрятана, сумма для соответствующей масти будет меньшей. Так, если вы закончили счетом 91-91-90-91, то это значит, что отсутствует туз треф. Отбрасывая двадцатки, можно, как и раньше, облегчить себе подсчет. При этом для получения числового значения отсутствующей карты последнюю найденную сумму нужно отнять от 11; если же она больше 11, то ее следует отнять от 31. (Впрочем, можно просто запомнить, что конечные суммы 20, 19 и 18 отвечают соответственно валету, даме и королю.)

Преимущество этого способа состоит в том, что удалять можно не одну карту, а сразу четыре — по одной каждой масти, при этом отгадать четыре карты будет не труднее, чем одну. В этом варианте королей можно не учитывать, так как заранее известно, что отсутствует по одной карте каждой масти. Конечной суммой для каждой масти теперь будет 78. (Короли не учитываются!) Отбросив три раза по 20, получим 18.

Таким образом, конечная цепочка 7-16-13-18 укажет, что отсутствуют следующие карты: валет пик, двойка черв, пятерка треф и король бубен.

Однако удерживать в памяти четыре меняющиеся цифры нелегко.

Чтобы обойти эту трудность, мы рекомендуем пользоваться в качестве «секретного» счетного приспособления… ногами. Если при раскладке карт вы сидите за столом и ваши ноги скрыты от присутствующих, то маловероятно, что небольшие шевеления ими которые здесь потребуются, будут кем-либо замечены.

В начале фокуса поставьте ноги так, чтобы подошвы ботинок прилегали к полу. Сдавая карту на стол, подымайте или опускайте носки ботинок по следующей системе. Появление карты пиковой масти отмечайте приподыманием или опусканием носка левого ботинка. Точнее говоря, с появлением первой такой карты приподымайте носок, второй — опускайте третьей — снова приподымайте, и т. д. Если карта червонной масти, то приподымайте или опускайте носок правого ботинка. Если карта окажется трефовой, то меняйте одновременно положение обоих носков. При появлении бубновой карты вообще не меняйте положения носков. После того как положена последняя карта, вы так узнаете масть отсутствующей карты: если левый носок на полу — карта красной масти, если приподнят — черной, если правый носок на полу, карта будет пиковой или бубновое масти; если правый носок приподнят — трефовой или червонной. Имея в виду вышесказанное, легко узнать масть спрятанной карты. Так, если оба носка на полу, карта будет бубновой масти. Если оба носка приподняты—трефовой масти, если приподнят один левый носок — пиковой, а если приподнят одни правый — червонной.

В качестве простейшего счетного приспособления при нахождении числовых значений карт можно использовать пальцы рук. Показывающий при этом держит руки на коленях, а карты (медленно) сдаются кем-нибудь из присутствующих. Пальцы перенумеровываются слева направо от 1 до 10. При появлении карты приподымается или опускается соответствующий палец. Валеты отмечаются перемещением левой руки вперед по ноге или назад, дамы — такими же движениями правой руки. Короли не принимаются во внимание. За мастями можно следить, двигая носками ботинок так, как это объяснялось выше.

Пользуясь пальцами как счетным приспособлением, можно находить числовые значения не только одной, но и нескольких вынутых из колоды карт, при условии, что эти значения не совпадают друг с другом. Для этого нужно лишь отметить, какие пальцы будут приподняты при окончанни раскладки (или какая рука продвинута вперед). Конечно, при этом нужно знать, сколько было спрятано карт, так как определить, что отсутствует король, можно только, не принимая во внимание при подсчетах одной карты.

Из колоды выбирают королей и дам и раскладывают их в две кучки: короли отдельно, дамы отдельно.

Кучки переворачивают лицевой стороной вниз и укладывают одну на другую. Зрители просят «снять» нашу колоду из восьми карт один или несколько раз.

Показывающий убирает кучку за спину и тут же открывает перед зрителями две карты. Оказывается, что это король и дама одной масти. С остальными тремя парами можно продемонстрировать то же самое.

Объяснение. Показывающему следует позаботиться лишь о том, чтобы в двух первоначальных кучках последовательность мастей была одинаковой.

«Снятие» этой последовательности не нарушит. За спиной показывающий только разделяет кучку строго пополам и получает нужные пары, беря в каждой половине верхнюю карту. В этой паре всегда окажутся король и дама одинаковой масти [6]).

Из колоды выбирают десять карт: пять красных и пять черных. Карты какого-нибудь одного цвета переворачиваются, и все десять карт тщательно тасуются зрителем. На мгновение показывающий убирает карты за спину. Затем он протягивает руки вперед, держит в каждой из них по пяти карт, которые тут же раскладываются на столе. Число открытых карт в каждой пятерке оказывается одинаковым, и эти карты будут различного цвета. Например, если в одной пятерке окажутся три красные карты, то в другой пятерке будут открытыми три черные карты. Фокус можно повторять сколько угодно раз, и он будет всегда удаваться.

Объяснение. Нетрудно сообразить, что среди карт одной пятерки будет открытых карт (а они одного цвета, например черного) столько же, сколько закрытых (красных) в другой пятерке.

За спиной следует просто разделить пачку пополам и, прежде чем показать карты зрителям, перевернуть одну из половин. Таким образом, благодаря тому, что карты перевернуты, число открытых карт в каждой пятерке будет одинаковым и эти карты будут разного цвета. В этом фокусе, конечно, можно пользоваться любым четным числом карт, нужно только, чтобы половина их была красной, а половина — черной.

Показывающий передает зрителю пачку в 18 карт и просит его проделать над ними под столом так, чтобы никто не видел, следующие операции: перевернуть верхнюю пару карт (т. е. две верхние карты, взятые вместе) и «снять» пачку, еще раз перевернуть верхнюю пару карт и снова снять. Так зритель может продолжать, сколько ему заблагорассудится. Ясно, что в результате этих действий карты перемещаются совершенно непредвиденным образом, причем ни число, ни положение открытых карт в колоде показывающему не могут быть известны. Затем показывающий, усевшись на противоположной от зрителя стороне стола, протягивает под столом руку и берет пачку. Оставляя руки под столом (так что никто, включая самого показывающего, не может видеть его действии над картами), он объявляет, что сейчас вынет пачку и в ней окажется столько-то открытых карт. Он называет число.

Карты вынимаются из-под стола и раскладываются.

Названное число оказывается правильным.

Объяснение. Фокус получается совершенно автоматически. Для того чтобы ои вышел, нужно лишь, спрятав карты под стол, пройтись по ним, переворачивая каждую вторую карту. После этого объявляется, что в пачке находится девять открытых карт (т. е. число, равное половине числа взятых карт). Фокус всегда получится, если для него брать любое четное число карт.

Показывающий просит кого-нибудь назвать число между 10 и 20 и откладывает одну за другой это число карт в кучку. Затем он находит сумму цифр названного числа, снимает сверху кучки число карт, равное этой сумме, и кладет их обратно на верх колоды.

Карта, оказавшаяся в кучке верхней, откладывается в сторону лицевой стороной вниз, а все остальные карты кучки возвращаются на верх колоды. Снова показывающий просит назвать любое число между 10 и 20 и проделывает то же самое вторично. Так третий и четвертый раз, пока этим способом не будут отобраны четыре карты. Эти четыре карты открываются — и все они оказываются тузами!

Объяснение. Перед началом фокуса тузы нужно положить на девятое, десятое, одиннадцатое и двенадцатое места сверху. Далее фокус получается автоматически [7]).

Зрителя просят снять колоду примерно посередине, взяв себе любую половину и пересчитать в ней карты.

Допустим, их 24. Два плюс четыре дает шесть. Зритель замечает в своей полуколоде шестую карту снизу, кладет эту полуколоду на другую и, подравняв карты, вручает их показывающему. Последний начинает сдавать карты по одной на стол, произнося при этом по-буквенно фразу «М-а-н-х-е-т-т-е-н-с-к-и-е ч-у-д-е-с-а» («The Magic of Manhattan»), причем так, чтобы на каждую положенную карту приходилось по одной букве. Вместе с последней буквой появится замеченная карта.

Объяснение. В результате описанной процедуры выбранная карта всегда оказывается на девятнадцатом месте сверху. Поэтому любая девятнадцатибуквенная фраза, например «П-о-р-а-з-и-т-е-л-ь-н-ы-е ф-о-к-у-с-ы», приводит к нужной карте [8]).

Пачку в 13 карт снимают несколько раз и передают зрителю. Показывающий поворачивается к зрителям спиной и просит переложить по одной любое число карт — от одной до тридцати включительно — снизу пачки наверх.

Показывающий поворачивается лицом к зрителям, берет пачку, развертывает ее веером лицевой стороной вниз и, не задумываясь, вытаскивает карту. Карта открывается, и все видят, что ее числовое значение равно числу переложенных карт. Этот фокус можно повторять сколько угодно раз.

Объяснение. Для демонстрации этого фокуса специально выбирают 13 карт так, чтобы на каждое целое число от 1 до 13 приходилась одна карта с соответствующим числовым значением. Их располагают в порядке убывания числовой величины, начиная с короля и кончая тузом. Показывающий снимает пачку несколько раз и передает ее зрителю, незаметно посмотрев на нижнюю карту. Допустим, это была четверка. После того как карты будут переложены, показывающнй отсчитывает сверху четыре карты и последнюю из них открывает. Ее числовое значение укажет число переложенных карт.[9]

Колода карт тасуется. Показывающий бегло ее просматривает, кладет лицевой стороной вниз и называет одну карту. Допустим, это двойка червей. Теперь кто-нибудь называет число от 1 до 26. Показывающий отсчитывает по одной это число карт на стол и открывает верхнюю карту положенной им кучки. Но это не двойка червей!

Показывающий принимает озадаченный вид и высказывает предположение, что карта, может быть, осталась в нижней половине колоды. Неверная карта поворачивается лицевой стороной вниз и кладется на эту полуколоду, а сверху помещаются остальные карты из кучки, оставшейся на столе. Зрителя просят назвать еще одно число, на этот раз от 26 до 52. Это число карт снова сдается на стол. И опять-таки оказывается, что верхняя карта в кучке — не двойка червей.

Показывающий принимает озадаченный вид и высказывает предположение, что карта, может быть, осталась в нижней половине колоды. Неверная карта поворачивается лицевой стороной вниз и кладется на эту полуколоду, а сверху помещаются остальные карты из кучки, оставшейся на столе. Зрителя просят назвать еще одно число, на этот раз от 26 до 52. Это число карт снова сдается на стол. И опять-таки оказывается, что верхняя карта в кучке — не двойка червей.

Опять неверная карта переворачивается и кладется на нижнюю часть колоды, а карты, взятые со стола, помещают сверху. Теперь показывающий высказывает предположение, что двойка червей найдется, если от второго числа отнять первое. Производится вычитание, и отсчитывается число карт, равное разности, следующая карта открывается, и на этот раз она оказывается двойкой червей!

Объяснение. Бегло просмотрев карты, показывающий просто называет верхнюю карту колоды. После двух отсчетов карта автоматически оказывается в положении, следующем за указываемым разностью двух чисел, названных зрителем [10]).

---

Пожалуй, почти каждый мелкий предмет, так или иначе связанный с числами или счетом, использовался для показа фокусов математического характера или для математических головоломок и задач. Самая большая группа таких фокусов — фокусы с игральными картами — была нами рассмотрена выше. В настоящей и последующих главах мы рассмотрим математические фокусы с другими мелкими предметами.

Не стараясь сделать изложение исчерпывающим, мы лишь проиллюстрируем различные принципы, на которых они основаны.

Игральные кости так же стары, как и игральный карты, а история зарождения этой игры так же неясна. И все же с удивлением приходится отметить, что самые ранние из известных игральных костей древней Греции, Египта и Востока имеют точно такой же вид, как и современные, т. е. кубик с цифрами от единицы до шестерки, нанесенными на грани кубика и расположенными таким образом, что сумма их на противоположных гранях равна семи. Однако кубическая форма игральной кости объясняется тем, что только правильный многогранник обеспечивает полное равноправие всех граней, а из пяти существующих в природе правильных многогранников куб обладает, явным преимуществом как атрибут игры: его легче всего изготовить, и, кроме того, он единственный из них, который перекатывается легко, но не слишком (тетраэдр перекатывать труднее, а октаэдр, икосаэдр и додекаэдр настолько близки по своей форме к шару, что быстро укатываются). Поскольку куб имеет шесть граней, то нанесение на них шести первых целых чисел напрашивается само собой, а расположение их с суммой — семеркой — представляется наиболее простым и симметричным. И это является между прочим единственным способом такого их попарно противоположного расположения, чтобы суммы всех пар были одинаковы.

Именно этот «принцип семерки» лежит в основе большинства математических фокусов с игральными костями. В лучших из таких фокусов упомянутый принцип применяется настолько тонко, что о нем никто и не подозревает. В качестве примера рассмотрим один очень старый фокус.

Показывающий поворачивается спиной к зрителям, а в это время кто-нибудь из них бросает на стол три кости. Затем зрителя просят сложить три выпавших числа, взять любую кость и прибавить число на нижней ее грани к только что полученной сумме.

Потом снова бросить эту же кость и выпавшее число опять прибавить к сумме. Показывающий обращает внимание зрителей на то, что ему никоим образом не может быть известно, какую из трех костей бросали дважды, затем собирает кости, встряхивает их в руке и тут же правильно называет конечную сумму.

Объяснение. Прежде чем собрать кости, показывающий складывает числа, обращенные кверху. Добавив к полученной сумме семерку, он находит конечную сумму.

Вот еще один остроумный фокус, основанный на принципе семерки. Показывающий, повернувшись спиной к зрителям, просит нх составить столбиком три игральные кости, затем сложить числа на двух соприкасающихся гранях верхней и средней костей, потом прибавить к полученному результату сумму чисел на соприкасающихся гранях средней и нижней костей, наконец, прибавить к последней сумме еще число на нижней грани нижней кости. В заключение столбик накрывается платком.

Теперь показывающий поворачивается к зрителям и вынимает из кармана горсть спичек, количество которых оказывается равным сумме, найденной зрителем при сложении пяти чисел на гранях кубиков.

Объяснение. Как только зритель сложит свои числа, показывающий на мгновение поворачивает голову через плечо якобы для того, чтобы попросить зрителя накрыть столбик платком. В самом же деле он в это время успевает заметить цифру на верхней грани верхнего кубика. Допустим, это шестерка.

В кармане всегда должна быть 21 спичка. Захватив все свои спички, показывающий, вынимая руку из кармана, роняет шесть из них обратно. Иными словами, он вытаскивает все спички без стольких, какова цифра наверху столбика. Это число спичек и даст сумму цифр на пяти гранях.

То обстоятельство, что зритель складывает числа на соприкасающихся гранях соседних кубиков, а не взаимно противоположные числа одного и того же кубика, служит хорошей маскировкой применения принципа семерки.

Этот фокус можно демонстрировать и без использования принципа семерки. Следует лишь заметить цифры на любых двух гранях каждого из кубиков. Дело в том, что существуют, только два различных способа нумерации костей, причем один из них является зеркальным отображением другого и, более того, все современные игральные кости нумеруются одинаково: если держать кубик так, чтобы была видна тройка 1, 2 и 3, то цифры в ней будут расположены в порядке, обратном движению часовой стрелки (рис. 1).

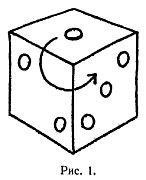
Рисуя себе мысленно взаимное расположение цифр 1, 2, 3 и вспоминая принцип семерки, чтобы представить себе местонахождение цифр 4, 5, 6, можно, глядя сбоку на столбик (верхнюю грань верхнего кубика предварительно накрывают монетой), правильно назвать число на верхней грани любого кубика. При хорошем пространственном воображении и небольшой практике этот фокус можно показывать с поразительной быстротой.

Много интересных фокусов с игральными костями связано с позиционным способом записи чисел. Вот типичный из таких фокусов. Зритель бросает три кости, причем показывающий не смотрит на стол. Число, выпавшее на одной из костей, умножается на два, к полученному произведению прибавляется пять, и результат снова умножается на пять. Число, выпавшее на второй кости, складывается с предыдущей суммой, и результат умножается на десять. Наконец, к последнему числу прибавляется число, выпавшее на третьей кости. Как только показывающий узнает окончательный результат, он немедленно называет три выпавших числа.

Объяснение. От последнего числа показывающий отнимает 250. Три цифры полученной разности и будут искомыми числами, выпавшими на костях.

Домино встречается в математических фокусах гораздо реже, чем карты и игральные кости. Весьма широко известен следующий фокус.

Показывающий записывает предсказание на листке бумаги и откладывает его в сторону. Косточки домино перемешивают, а затем выкладывают цепочкой, приставляя одинаковые концы друг к другу, как это делается при обычнбй игре в домино. После окончания раскладки смотрят на число очков на каждом из концов цепи. Достают листок бумаги, и оказывается, что там записаны как раз эти два числа! Фокус повторяете несколько раз, причем каждый раз предсказываются новые цифры.

Объяснение. Этот фокус получается потому, что любая цепочка, составленная из всех без исключения косточек домино (их бывает обычно 28), имеет одинаковое число очков на концах [11]). Показывающий перед началом фокуса незаметно прячет одну косточку, а числа очков на концах ее записывает в предсказании. Так как при выкладывании всех 28 косточек должна образоваться замкнутая цепочка, то отсутствующая косточка укажет числа очков на месте ее разрыва. Удаляемая косточка не должна быть дублем.

Вот еще один любопытный фокус с домино. Для него нужны 13 косточек, которые укладываются в ряд лицевой стороной вниз. В отсутствие показывающего, кто-нибудь из зрителей передвигает по одной любое число косточек (от одной до двенадцати) с одного конца ряда на другой. После этого показывающий возвращается в комнату, открывает одну косточку, и количество очков на ней оказывается равным числу перемещенных косточек. Фокус можно показывать сколько угодно раз.

Объяснение. Косточки, конечно, подбираются специальным образом. Суммы очков на них должны последовательно равняться всем целым числам от 1 до 12. Тринадцатой будет двойная пустышка.

Они выставляются в порядке возрастания, начиная с единицы на левом конце. Справа ряд замыкается двойной пустышкой. Перед уходом из комнаты показывающий демонстрирует, как нужно перемешать косточки; передвинув несколько штук слева направо, он должен сообразить, сколько очков теперь на самой левой косточке. Возвратившись, он мысленно считает до этого числа, начиная справа. Если на левой косточке было, например, 6 очков, ему нужно считать справа до шестой косточки. Косточку, на которую придется это число, он открывает. Если она случайно окажется двойной пустышкой, ей приписывается значение 13.

Повторять этот фокус совсем просто. Показывающий должен сосчитать про себя, сколько косточек осталось от открытой до крайней левой, сообразить, сколько на последней очков, и запомнить это число перед уходом из комнаты.

Любопытная ситуация возникает, если кто-нибудь вздумает подшутить над показывающим и не переставит ни одной косточки; в этом случае откроется двойная пустышка.
Календари

Существует много интересных фокусов с использованием табель-календаря. Вот некоторые наиболее интересные из них.

Показывающий стоит, повернувшись спиной к зрителям, а один из них выбирает на помесячном табель-календаре любой месяц и отмечает на нем какой-нибудь квадрат, содержащий 9 чисел. Теперь достаточно зрителю назвать наименьшее из них, чтобы показывающий тут же, после быстрого подсчета, объявил сумму этих девяти чисел.

Объяснение. Показывающему нужно прибавить к названному числу 8 и результат умножить на 9 [12]).

Фокус с отмеченными датами

Фокус начинается так. Зрителю предлагают открыть помесячный табель-календарь на любом месяце и обвести кружком по своему выбору по одной дате в каждом из пяти столбиков. (В том случае, когда числа располагаются в шести столбиках, что бывает весьма редко, шестой столбик не принимают во внимание.)

При этом показывающий стоит спиной к присутствующим.

Все еще не оборачиваясь, он спрашивает: «Сколько у Вас обведено понедельников?», затем: «Сколько вторников?» и т. д., перебирая все дни недели. После седьмого и последнего вопроса показывающий объявляет сумму цифр, обведенных кружочками.

Объяснение. Сумма чисел в строке, которая начинается первым числом месяца, всегда равна 75 (за исключением февраля не високосного года). Каждое отмеченное число в следующей строке увеличивает эту сумму на 1, в следующей за ней строке на 2 и т. д.; каждое отмеченное число в предыдущей строке уменьшает упомянутую сумму на 1, в предшествующей ей строке на 2 и т. д. Пусть, например, первое число месяца приходится на четверг и обведены один понедельник, один четверг и три субботы; показывающий производит в уме вычисление:

75 + 3х2 – 1х3 = 78

и объявляет полученный результат.

Разумеется, показывающий должен знать заранее, на какой день приходится первое число выбранного зрителем месяца.

На каком-нибудь листке помесячного табель-календаря зритель заключает в квадрат шестнадцать чисел. Показывающий после беглого взгляда на обведенную фигуру записывает предсказание. Затем зритель выбирает в этом квадрате четыре числа, по видимости произвольных, но с соблюдением следующего правила. Первое из чисел выбирается (обводится кружочком) совершенно произвольно. Затем вычеркиваются все числа, находящиеся в той же строчке и в том же столбце, что и только что обведенное число. В качестве второго числа зритель может обвести кружочком любое число, оставшееся незачеркнутым. После этого он вычеркивает все числа, оказавшиеся в одной и той же строчке и в одном и том же столбце со вторым обведенным числом. Так же выбирается третье число, а соответствующие строчка и столбец вычеркиваются.

В результате этих операций останется незачеркнутым одно-единственное число. Его зритель также обводит кружочком. Если теперь взять сумму четырех отмеченных нами чисел, то она окажется в точности равной предсказанному числу [13]

Объяснение. Показывающий замечает два числа, находящихся на двух диагонально противоположных углах квадрата. Какая из двух возможных пар это будет — безразлично. Чтобы получить ответ, нужно сложить эти два числа и найденную сумму удвоить.

Более простой фокус, основанный на этом же принципе и не требующий табель-календаря, можно демонстрировать так. Начертите квадратную сетку из 16 клеток, подобную шахматной доске, и перенумеруйте клетки от 1 до 16 в естественном порядке. Если теперь предложить зрителю выбрать четыре числа при помощи того процесса, который описывался выше, и сложить их, то во всех случаях он будет получать одну и ту же сумму, а именно 34. Этот принцип можно демонстрировать на квадратах с любым числом клеток.

Зритель задумывает какое-нибудь число от 1 до 12. Показывающий начинает притрагиваться кончиком карандаша к числам ни циферблате, делая это, по-видимому, в совершенно произвольном порядке. В это время зритель считает про себя, начиная с задуманного числа до двадцати, причем так, чтобы на каждое прикосновение показывающего к часам приходилось одно число. Дойдя до 20, он произносит «стоп». И (странное совпадение!) карандаш оказывается в этот момент как раз на задуманном числе.

Объяснение. Первые восемь прикосновений действительно делаются совершенно наугад. Однако уже на девятом показывающий должен обязательно коснуться 12 и с этого момента перебирать часы строго подряд в направлении, обратном движению часовых стрелок. Когда зритель произнесет слово «стоп», кончик карандаша будет указывать на требуемое число [14]).

Совсем не обязательно просить зрителя прекращать счет именно на 20, вы можете предложить ему самому выбрать число для окончания счета: нужно лишь, чтобы оно было больше 12. Конечно, зритель должен предупредить вас, на каком числе он собирается остановиться. Отнимите от этого числа 32, и полученный остаток укажет, сколько прикосновений нужно сделать наугад, прежде чем притронуться к 12 и начать двигаться последовательно против часовой стрелки.

Принцип «последовательного счета», с которым мы только что встретились, применяется и во многих других фокусах. Например, такой фокус. Присутствующие называют 16 слов, каждое из которых пишется на отдельном листе плотной бумаги, обратные стороны этих листков помечают буквами от «А» до «Р» (пропуская «неудобные» буквы «Ё» и «Й»). Листки перемешиваются на столе. Показывающий поворачивается спиной, а кто-нибудь из присутствующих выбирает один из листков, запоминает слово и букву на нем, а затем смешивает с остальными. Показывающий собирает листки и раскрывает их веером так, чтобы присутствующие видели слова. Потом он начинает бросать листки на стол по одному без видимой системы, зритель же в это время называет про себя буквы в алфавитном порядке, начиная с той, которой помечено задуманное им слово. Дойдя до «Р», он произносит «стоп». На листке, который как раз в этот момент бросает на стол показывающий, оказывается задуманное слово.

Чтобы этот фокус получился, нужно бросать листки на стол в порядке, обратном алфавитному, начиная с буквы «Р».

Вот еще один фокус с часами. Показывающий отворачивается от стола, а в это время зритель бросает кость и задумывает какое-нибудь число (желательно не большее 50, чтобы не затягивать фокус). Допустим, это 19. Далее зритель начинает притрагиваться к цифрам на циферблате, начав с числа, указанного игральной костью, и двигаясь по часовой стрелке.

Число, на которое придется последнее 19-е касание, записывается. Затем он снова делает 19 прикосновений, но уже в направлении, обратном движению часовой стрелки, отсчитывая их с той же цифры, что и в предыдущий раз. Число, на которое придется последнее прикосновение, опять записывается. Оба записанных числа складываются, и сумма их называется вслух. После этого показывающий сразу называет число, выпавшее на игральной кости [15]).

Объяснение. Если названная сумма меньше или равна 12, то для получения ответа нужно просто разделить ее на 2. Если же сумма больше 12, то показывающий сначала вычитает из нее 12, а затем уже делит остаток на 2.

Существует много математических фокусов, в которых мелкие предметы используются просто как счетные единицы. Сейчас мы опишем несколько фокусов, для которых особенно удобны спички, хотя годятся и другие мелкие предметы, например монеты, камешки или листочки бумаги.

Показывающий поворачивается спиной к аудитории, а кто-нибудь из присутствующих кладет на стол три кучки спичек так, чтобы число спичек в кучках было одинаковым и большим трех в каждой. Зритель называет какое-нибудь число от 1 до 12. Показывающий просит зрителя перераспределить некоторым (специальным) образом спички в кучках. При этом, хотя показывающий и не знал первоначального числа спичек в кучках, в средней кучке оказывается заданное количество спичек.

Объяснение. Вначале зрителя просят взять по три спички из крайних кучек и перенести их в среднюю. Затем он должен сосчитать оставшиеся спички в одной из крайних кучек, взять это число спичек из средней кучки и перенести их в любую крайнюю. Так как после этого в средней кучке всегда остается 9 спичек [16]), то теперь уже совсем просто получить в ней заданное число спичек (для этого потребуется только одна передвижка).

На аналогичном принципе основан следующий фокус, для показа которого необходим коробок с 20 спичками. Показывающий, повернувшись спиной к зрителю, просит его вытянуть из коробка несколько спичек (не больше десяти) и положить в карман. Затем зритель пересчитывает оставшиеся в коробке спички. Допустим, их 14. Это число он «выписывает» на столе следующим образом: единица изображается одной спичкой, положенной слева, а четверка — четырьмя спичками, положенными несколько правее. Эти пять спичек берутся из числа оставшихся в коробке.

После этого спички, изображавшие число 14, также кладутся в карман. В заключение зритель вынимает из коробка еще несколько спичек и зажимает их в кулаке.

Показывающий поворачивается лицом к зрителям, высыпает спички из коробки на стол и сразу называет число спичек, зажатых в кулаке.

Объяснение. Чтобы получить ответ, нужно вычесть из девятки число спичек, рассыпанных на столе [17]).

Еще один старинный фокус можно показать на 24 спичках, которые складываются кучкой рядом с тремя небольшими предметами, скажем, монетой, кольцом и ключиком. В фокусе просят принять участие трех зрителей (будем называть их условно 1, 2, 3).

Первый зритель получает одну спичку, второй — две, третий — три. Вы поворачиваетесь к ним спиной и просите каждого взять по вещице из лежащих на столе (обозначим их А, Б и В).

Предложите теперь зрителю, держащему предмет А, взять ровно столько спичек из числа оставшихся в кучке, сколько у него на руках. Зритель, взявши Б, пусть возьмет дважды столько спичек, сколько у него на руках. Последнему зрителю, взявшему предмет В, предложите взять четырежды столько спичек, сколько у него на руках. После этого пусть все три зрителя положат свои предметы и спички в карманы.

Обернувшись к зрителям и взглянув на оставшиеся спички, вы сразу же говорите каждому зрителю, какой предмет он взял.

Объяснение. Если остается одна спичка, то зрители 1, 2 и 3 взяли соответственно предметы А, Б и В (именно в таком порядке).

Если осталось 2 спички, то порядок предметов будет Б, А, В.

Если осталось 3 спички, то А, В, Б.

Если 4 спички, то кто-то ошибся, так как подобный остаток невозможен.

Если 5, то порядок предметов будет Б, В, А.

Если 6, то В, А, Б.

Если 7, то В, Б, А [18]).

Удобным мнемоническим средством будет список слов, согласные буквы которых (в порядке их написания) соответствуют начальным буквам названий трех выбранных предметов. Так, например, если показывать фокус с ложкой, вилкой и ножом, то можно предложить следующий список слов:

1. Л и В е Н ь.

2. Л е Н и В е ц.

3. В о Л а Н.

5. В а Н и Л ь.

6. Н е В о Л я.

7. Н а Л и В к а.

Здесь буква «Л» должна обозначать ложку, «В» — вилку, «Н» — нож. Буквы расположены в словах в порядке, соответствующем порядку предметов. Числа, стоящие перед словами, обозначают число оставшихся спичек.

Монеты обладают тремя свойствами, которые делают их удобными для демонстрации математических фокусов. Их можно использовать как счетные единицы, они обладают определенным числовым значением и, наконец, у них есть лицевая и обратная стороны.

В каждом из следующих трех фокусов демонстрируется какое-нибудь одно из этих трех свойств.

Дюжина (или больше) монет размещается на столе в форме девятки (рис. 2).

Показывающий стоит, повернувшись спиной к зрителям. Кто-нибудь из присутствующих задумывает число, большее числа монет в «ножке» девятки, и начинает отсчитывать монеты снизу вверх по ножке и, далее, по колечку против часовой стрелки, пока не дойдет до задуманного числа. Затем он снова считает от единицы до задуманного числа, начав с монеты, на которой остановился, но на этот раз по часовой стрелке и только вокруг колечка.

Под монету, на которой закончился счет, прячется маленький кусочек бумажки. Показывающий поворачивается к столу и сразу же поднимает эту монету.

Объяснение. Независимо от того, какое число было задумано, счет заканчивается всегда на одной и той же монете.[19] Сначала сами проделайте все это в уме с любым числом, чтобы узнать, какая это будет монета. При повторении фокуса добавьте к ножке несколько монет, тогда счет закончится уже в другом месте.

Вот старинный фокус, в котором используется числовое значение монеты. Попросите кого-нибудь взять в один кулак гривенник, а в другой — копейку. Затем предложите умножить числовое значение монеты, лежащей в правом кулаке, на восемь (или любое другое четное число), а числовое значение другой монеты на пять (или любое нечетное число, какое вам захочется). Сложив эти два числа, зритель должен сказать вам, четное или нечетное число получилось. После этого вы говорите ему, какая монета у него в какой руке.

Объяснение. Если сумма четная, то в правой руке — копейка; если нечетная — гривенник.

Интересный фокус, основанный на разнице между двумя сторонами монеты, гербом и «решеткой», начинается с того, что на стол высыпается горсть мелочи. Показывающий отворачивается и просит кого-нибудь из зрителей заняться перевертыванием монет по одной наугад, произнося при каждом перевертывании «есть».

При этом зритель может переворачивать одну и ту же монету по нескольку раз. Затем зритель накрывает ладонью одну из монет. Показывающий поворачивается к столу и говорит, как лежит закрытая монета, кверху гербом или «решеткой».

Объяснение. Перед тем как отвернуться, вам нужно сосчитать число гербов. При каждом слове «есть» прибавляйте к этому числу единицу. Если последняя сумма четная, то число гербов, после того как зритель закончит перевертывание монет, тоже будет четным; если сумма нечетная, то нечетным.

Посмотрев на открытые монеты, совсем нетрудно определить, как лежит монета под ладонью, кверху гербом или «решеткой».

Этот фокус можно показывать с набором любых одинаковых предметов, которые можно расположить на столе одним из двух возможных способов, например с крышечками от бутылок с лимонадом, листочками бумаги, одна сторона которых помечена крестиком, игральными картами, спичечными коробками и т. п.

Пока показывающий стоит, отвернувшись от доски, зритель берет три шашки и расставляет их на доске либо по диагонали, отмеченной на рис. 3 тремя буквами А, либо на противоположной диагонали, отмеченной тремя буквами 5, и начинает передвигать их, произнося про себя буквы своего имени или фамилии (или и те и другие).

При этом на каждую букву должен приходиться только один ход, который можно делать любой шашкой в любом направлении на одну клетку (шашки передвигаются только по белым полям).

Послетого как вся фамилия будет произнесена, зритель может повторить всю процедуру еще несколько раз, опять-таки выбирая шашки наугад. После этого показывающий поворачивается к зрителям и, мельком взглянув на доску, объявляет, с какого угла зритель начинал передвигать шашки: с левого верхнего или правого нижнего.

Объяснение. Имя и фамилия, которые нужно побуквенно произносить про себя, должны обязательно состоять из четного числа букв. Если и имя и фамилия зрителя содержат такое число букв, можно брать как то, так и другое. Если четное число букв имеет только одно из таких слов, то предложите произносить именно это слово. Если, наконец, оба слова состоят из нечетнего числа букв, то они должны произноситься друг за другом (так как сумма двух нечетных чисел четна).

Повернувшись к зрителям и взглянув на доску, обратите внимание на вертикальные четные ряды, считая их занумерованными, как на рисунке. Если в этих рядах окажется всего четное число шашек (т. е. две или ни одной), то вначале шашки стояли в правом нижнем углу, в противном случае — в левом верхнем [20]).

Три различных предмета кладутся на столе в ряд, и занимаемые ими места (не сами предметы, а лишь места) обозначаются цифрами 1, 2 и 3. Показывающий поворачивается к зрителям спиной, а кто-нибудь из присутствующих начинает попарно менять местами предметы, называя при этом лишь соответствующие местам цифры. Так, например, переставляя предметы, стоящие на первом и третьем местах, он произносит вслух «один и три». Таким образом, зритель может передвигать предметы сколько угодно раз, но обязательно называя при этом соответствующие цифры.

Когда же он, наконец, устанет от этого занятия, он задумывает какой-нибудь предмет и меняет местами два других предмета, ничего не говоря показывающему. Далее он снова начинает попарно переставлять предметы произвольным образом, но опять называя вслух соответствующие цифры. Так зритель может продолжать, пока ему не надоест. В конце концов показывающий поворачивается к столу и немедленно указывает задуманный предмет.

Объяснение. Стоя спиной к столу, вы незаметно для зрителя пользуетесь в качестве счетного приспособления какой-нибудь рукой. Пусть три пальца (например, указательный, средний и безымянный) обозначают цифры 1, 2 и 3. Перед тем как отвернуться от предметов, заметьте положение одного из них. Допустим, что вы взяли для показа фокуса кольцо, карандаш и монету и кольцо занимает положение 1.

Тогда коснитесь большим пальцем того пальца, которому вы приписали цифру 1. По мере того как зритель будет сообщать вслух о своих перестановках, вы должны передвигать большой палец по пальцам, обозначающим цифры, следя при этом только за положением кольца. Так, если первая перестановка включала 1 и 3, вы перемещаете большой палец на палец под номером 3.

Если же перестановка включала 2 и 3, не затрагивая таким образом кольца, то вы ничего не делаете, оставляя большой палец на прежнем месте.

После того как зритель задумал предмет и сделал неизвестную вам передвижку остальных двух, он снова начинает называть вслух цифры, обозначающие перестановки. При этом вы продолжаете следить за положением кольца, как если бы оно не изменилось в результате неизвестной вам передвижки.

В заключение всех операций по перестановкам ваш большой палец остановится на каком-то пальце.

Допустим, что этот палец имеет номер 2. Взгляните на второе место на столе. Если там окажется кольцо, вы сразу же определяете, что было задумано именно кольцо, потому что его положение не изменилось в результате неизвестной вам передвижки.

Если же кольцо оказывается не там, где это указывает вам большой палец, то взгляните на два других предмета (кольцо и еще что-то), тот другой предмет (не кольцо) и будет задуманным.

Наш метод поразительно прост и легко догадаться, почему он приводит к цели. По сути, мы здесь имеем дело с задачей элементарной логики, где пальцы выполняют роль простейшей логической машины.

Вот еще один увлекательный фокус, имеющий своим источником только что описанный фокус; он выглядит так: четыре спички располагаются на столе в ряд, три из них обращены головками в одну сторону, а четвертая, чтобы выделить ее среди остальных, — в противоположную. Показывающий стоит, повернувшись к зрителям спиной, а кто-нибудь из присутствующих переставляет спички на первый взгляд совсем произвольным образом. Все еще не поворачиваясь к зрителям, показывающий просит убрать сначала одну спичку, потом еще одну и, наконец, третью, оставляя таким образом на столе только одну спичку.

И эта оставшаяся спичка обязательно оказывается повернутой!

Этот фокус можно повторять много раз, и он всегда будет удаваться. Его можно показывать на любых четырех предметах, поэтому мы описываем его в этом разделе, а не там, где фокусы со спичками.

Объяснение. Положение спичек или предметов, расположенных на столе, обозначьте цифрами 1, 2, 3 и 4. Попросите кого-нибудь указать один из этих предметов. Прежде чем вы повернетесь к зрителям спиной, запомните его положение. Теперь попросите сделать пять перестановок, меняя при этом местами выбранный предмет с соседним. Если был указан предмет, находящийся на одном из концов, то, конечно, первую перестановку можно выполнить единственным образом; если же был указан не крайний предмет, то его можно переставить либо с правым соседним предметом, либо с левым.

Поскольку зритель не сообщает показывающему, как он меняет местами предметы, может возникнуть представление, что после данного числа перестановок выбранный предмет может занять любое место в ряду.

Однако это не так. Например, если указанный предмет занимал 2-е или 4-е (т. е. четное) место, то после пяти перестановок он может оказаться либо на 1-м, либо на 3-м (т. е. нечетном) месте. Наоборот, если мы начнем с 1-го или 3-го места, то придем ко 2-му или 4-му.

При нечетном числе перестановок так будет получаться всегда. В нашем примере мы предложили сделать пять перестановок, но можно было назначить семь или, скажем, двадцать девять (любое нечетное число) перестановок. Мы могли бы также задать четное число перестановок, но в этом случае выбранный предмет очутился бы на четном месте, если он был на четном вначале, или на нечетном, если на таком же месте он был вначале. Вопрос о числе перестановок может решать и сам зритель, хотя, конечно, это число он должен вам сообщить. Можно также, переставляя предметы, произносить по буквам свое имя и фамилию.

После того как перестановки будут закончены, вы должны указать зрителю, в каком порядке он должен поштучно убирать. три предмета, чтобы на столе остался четвертый выбранный. Это нужно делать так: Если вам известно, что указанный предмет может оказаться после окончания передвижек на 1-м или 3-м месте, то сначала попросите убрать предмет, находящийся на 4-м месте. Затем попросите зрителя поменять местами выбранный предмет с соседним. В результате этой последней перестановки указанный вам предмет всегда окажется средним из трех оставшихся. Теперь уже не составляет никакого труда оставить на столе выбранный зрителем предмет.

Если же, наоборот, конечное положение указанного предмета может быть 2-м или 4-м, то сначала следует убрать предмет, находящийся на 1-м месте, а все остальное происходит так же.

---

В предыдущих главах мы рассматривали только такие фокусы, метод показа которых носит математический характер. Мы не занимались фокусами, в которых только конечный результат может быть объяснен при помощи математики. Если, например, показывающий, играя в карты, набирает нужное число взяток, заранее расположив карты в колоде соответствующим образом, то этот эффект можно считать математическим в том смысле, что произвольное расположение карт в колоде каким-то непостижимым образом стало упорядоченным, но мы такой фокус все же не будем называть математическим, поскольку показ его основан не на математике, а просто на незаметной подмене одной колоды другой.

Подобный подход мы применим и к отбору фокусов для настоящей главы. Очень многие «таинственные» фокусы можно назвать в широком смысле топологическими, так как при их показе как будто нарушаются элементарные топологические законы. Один из самых старинных фокусов такого рода известен под названием «соединенных колец»: шесть или более больших железных колец таинственным образом сцепляются и расцепляются — явление, кажущееся совершенно невозможным в силу свойств обычных замкнутых кривых линий. Другие фокусы, в которых кольца снимаются или надеваются на веревку или палку, оба конца которой зажаты в руках зрителя, можно было бы объяснить таинственными соединениями или разрывами цепи, поскольку зритель, держащий веревку, представляет собой замкнутую линию, через которую как-то проходит наше кольцо. Однако большинство таких фокусов основано на механических методах, небольшой ловкости рук или других «таинственных» приемах, ничего общего не имеющих с топологией.

Более близок к тому, что может быть названо топологической головоломкой, фокус, который известен под названием «падающее кольцо». Это цепочка колец, связанных друг с другом довольно странным образом. При надлежащих действиях верхнее кольцо как будто падает по цепи, пока, наконец, не оказывается странным образом соединенным с самым нижним кольцом. Этот фокус получается сам собой, и при его показе не возникает никаких затруднений, если не считать того, что кольца должны быть соединены так, чтобы они образовали некоторую сложную и довольно любопытную топологическую структуру.

«Падение» кольца в этом фокусе является лишь оптической иллюзией, объясняемой механически и не связанной с топологическими законами.

Весь материал этой главы будет включать в себя только фокусы, которые по методам показа могут рассматриваться как топологические. Так как топология занимается такими свойствами тел (предметов), которые не изменяются при непрерывных преобразованиях (растяжениях и сжатиях), при показе топологических фокусов (как и естественно ожидать) придется ограничиться почти исключительно таким гибким материалом, как бумага, ткани, нитки, бечевки и резиновые ленты.

Хорошо всем известный «лист Мёбиуса», названный по имени Августа Фердинанда Мёбиуса, немецкого астронома и пионера-тополога, впервые описавшего эту поверхность, используется на протяжении последних 75 лет для многих фокусов. В одном из них показывающий вручает зрителю три больших бумажных кольца, каждое из которых получилось путем склеивания концов длинной бумажной ленты. Зритель разрезает ножницами первое кольцо вдоль ленты посередине, пока не вернется в исходную точку. В результате получаются два отдельных кольца. Разрезая таким же образом второе кольцо, он получает, к своему удивлению, не два кольца, а одно, которое вдвое длиннее исходного. Наконец, разрезая третье, он снова получает поразительный результат: два кольца, сцепленных друг с другом.

Результат этого фокуса зависит от того, как были сомкнуты концы ленты перед склейкой. Первое наше кольцо получилось путем простого соединения концов ленты без перекручивания. Второе кольцо (его называют листом Мёбиуса) получается при соединении концов ленты, перекрученной один раз на 180°. Одним из наиболее любопытных свойств этой поверхности, имеющей только одну сторону и один край, является то, что, разрезая ее вдоль посередине, мы получаем одно большое кольцо, если же разрезать его не посередине, а на расстоянии в одну треть ширины от края, то получается два кольца: одно большое и сцепленное с ним маленькое. Третье кольцо получилось при разрезании ленты, концы которой перекручивались перед склейкой дважды, т. е. на 360°.

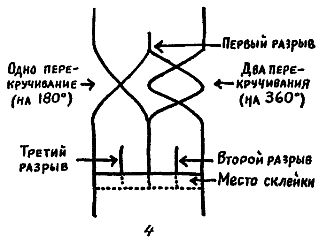
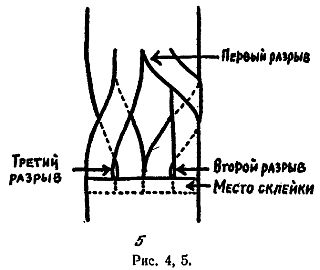
В другом варианте фокуса кольцо разрезается на два отдельных кольца, одно из которых при разрезании посередине превращается тоже в два отдельных кольца, а другое — в одно большое. Оригинальный метод приготовления кольца для такого фокуса показан на рис. 4, а его улучшение — на рис. 5. Для склеивания концов употребляется какой-нибудь быстросохнущий клей.

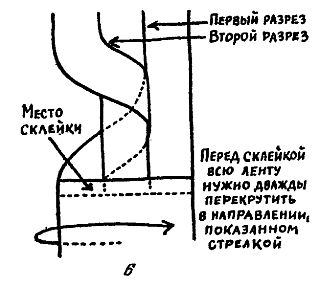
Способ приготовления бумажной ленты, при котором после двух разрезов получается цепочка из трех сцепленных колец, изображен на рис. 6.

Если изготовить кольцо так, как показано на рис. 7, то после первого разрывания (разрезания) получится большое кольцо, размер которого вдвое больше первоначального, а второе разрывание даст кольцо вчетверо длиннее исходного.

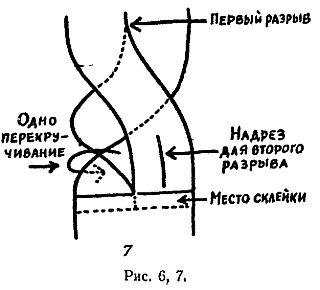
Другой вариант изображен на рис. 8, первое разрывание дает одно большое кольцо, а второе — два сцепленных.

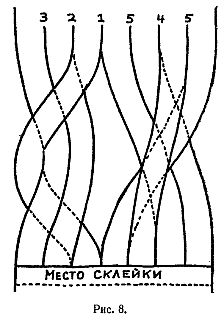
Можно придумать и другие комбинации. Например, после разрывания кольца, изображенного на рис. 9, получаются два отдельных кольца. Разрывание одного из них дает цепочку из трех колец, разрывание другого — одно большое кольцо. Это последнее кольцо можно разрывать еще раз, причем получится еще большее кольцо.

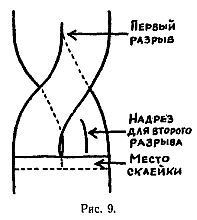
Если трижды перекрученную ленту продеть сквозь перстень, склеить концы, а затем разрезать или разорвать вдоль посередине, то получится одно большое кольцо с узлом, завязанным вокруг перстня.

Можно отыскать свыше десятка современных фокусов топологического характера с носовыми платками.

Вот вариант одного из наиболее старых таких фокусов.

Показывающий берет носовой платок за противоположные углы и вращает его как детскую скакалку, пока он как следует не перекрутится. Скрученный платок вешается на вытянутый указательный палец правой руки зрителя, как это показано на рис. 10.

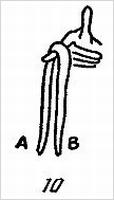
Обернув платок вокруг пальца, показывающий просит зрителя положить левый указательный палец на правый, после чего платок плотно обтягивается вокруг обоих пальцев (см. далее рис. 11–16).

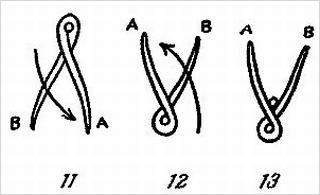
Затем показывающий, удерживая указательный палец правой руки зрителя за кончик (рис. 17), просит его вытянуть из платка другой (верхний) указательный палец. После этого показывающий тянет концы платка вверх и платок свободно стягивается с оставшегося в нем пальца, как бы перерезая его.

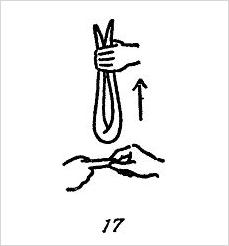
Объяснение. Хотя в этом фокусе и кажется, что платок надежно стягивает оба пальца, в действительности же при таком способе обвязывания правый указательный палец остается вне петли, образуемой платком.

Делается это так.

1. Скрестите концы платка под пальцем (рис. 11). Заметьте, что конец, помеченный буквой А, расположен (в точке скрещивания) ближе к вам, чем конец В.

Так должно быть и при всех дальнейших операциях, иначе фокус не получится.

2. Подымите концы платка вверх (рис. 12) и скрестите их там.

3. Попросите зрителя положить указательный палец левой руки на пересечение (рис. 13).

4. Скрестите сверху концы платка, следя за тем, чтобы конец А был ближе к вам (рис. 14).

5. Опустите концы вниз и скрестите их там (рис. 15).

6. Подымите снова концы вверх и возьмите их в левую руку (рис. 16). Теперь будет казаться, что пальцы надежно стянуты.

7. Зажмите конец нижнего указательного пальца.

Попросите зрителя вытянуть другой указательный палец.

Потяните платок вверх, и он свободно сойдет с оставшегося в нем пальца (рис. 17).

Два платка, желательно контрастных цветов, крепко скручивают и берут в левую руку так, как изображено на рис. 18.

Правая рука подводится под темный платок, зажимает конец А светлого платка и обертывает его один раз вокруг темного платка (рис. 19).

Конец В темного платка проносится за светлый платок, а затем выносится вперед, как это показано на рис. 20.

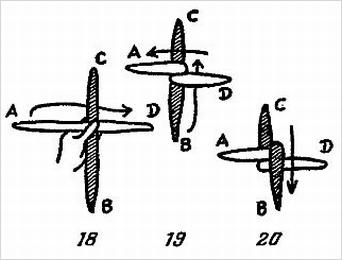
Концы В и С соединяются друг с другом внизу и берутся в правую руку. Концы А и D соединяются наверху и берутся в левую руку (рис. 21).

Зрителям будет казаться, что платки надежно связаны, но стоит только потянуть за концы, как они легко разъединяются. Большие шелковые платки можно дважды обертывать друг около друга и затем все же легко разъединять.

Оба эти фокуса основаны на следующем принципе: одна серия «завертываний» как бы уничтожается другой серией «развертываний». Этот же принцип встречается в ряде фокусов со шнурками, которые можно обкрутить вокруг ноги, стержня или палки, а затем свободно снять, как бы разрезая эти предметы.

Вот еще одна довольно известная головоломка топологического характера: как завязать на платке узел, не выпуская из рук его концов. Это можно сделать так. Скрутите платок жгутом и положите его на стол. Скрестите руки на груди. Продолжая держать их в этом положении, нагнитесь к столу и возьмите поочередно по одному концу платка каждой рукой. После того как руки будут разведены, в середине платка сам собой получится узел. Пользуясь топологической терминологией, можно сказать, что руки зрителя, его корпус и носовой платок образуют замкнутую кривую в виде «трехлистного» узла.

При разведении рук узел только перемещается с рук на платок.

Занимательный вариант этой головоломки можно демонстрировать с помощью шнура, шарфа или галстука. Уложите, например, галстук на столе так, как это изображено на рис. 22.

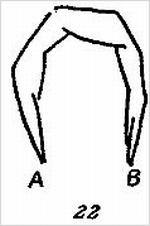
Возьмите конец В правой рукой и попросите зрителя внимательно следить за тем, как вы завязываете узел. Пропустите теперь левую руку под конец В ладонью вниз (рис. 23),

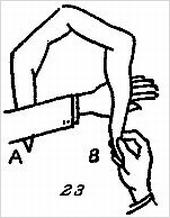
а затем выверните ее назад, как это показано на рис. 24,

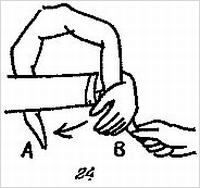
и подберите конец А. После того как вы разведете руки, на галстуке получится узел. Как ни странно, но такие движения довольно трудно воспроизвести. Вы можете снова и снова показывать фокус присутствующим, но когда они попытаются проделать его сами, узлы завязыцаться не будут.

Показывающий раскладывает на столе шнур замысловатым образом, а зритель пытается поставить внутрь одной из образовавшихся петель свой палец так, чтобы он оказался захваченным, когда фокусник начнет стягивать шнур со стола. Существует много остроумных способов укладки шнура, позволяющих фокуснику быть хозяином в этой игре, т. е. либо захватывать палец зрителя, либо оставлять его свободным, независимо от того, куда зритель поставит его.

На рис. 25 дан простейший вариант с двумя петлями.

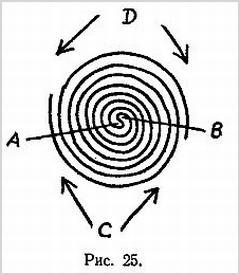
Независимо от того, какую из них, А или В, изберет зритель, показывающий может дать ему выиграть или проиграть, собирая тем или иным способом концы шнура.

На рис. 25 эти два способа указаны соответственно стрелками С и D. Этот фокус удобно показывать также при помощи пояса, который сначала складывается вдвое, а затем скручивается в спираль вокруг большого и указательного пальцев (один из которых предварительно вставляется в петлю). Зритель обыкновенно старается уследить за петлей, в которую вначале был поставлен палец показывающего. Однако в какое бы место зритель ни поставил затем свой палец, считая, что он ставит его в петлю, показывающий может стянуть пояс беспрепятственно. Здесь, как и в случае со шнуром, показывающий по желанию может либо свободно стянуть пояс с пальца, либо оставить палец захваченным.

Для показа другого занимательного фокуса нужен шнур и бечевка длиной не менее 6 м. Концы этого шнура связывают узлом, чтобы получилась замкнутая кривая, и кого-нибудь из присутствующих просят уложить шнур на ковре так, чтобы образовался сколь угодно сложный узор (рис. 26), но с условием, чтобы в нем не было самопересечений.

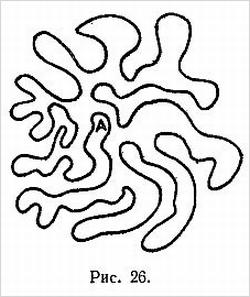
Затем по краям узора укладывают газеты, так что видимой остается лишь его внутренняя прямоугольная часть (рис. 27).

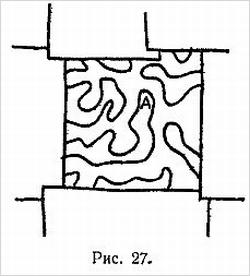
Теперь зритель ставит палец и держит его прижатым в любом месте узора. Вопрос состоит в следующем: если убрать одну из газет и потянуть наружу за какую-нибудь часть шнура, бывшую под газетой, будет при этом палец зрителя захвачен шнуром или же он останется свободным? Принимая во внимание сложность узора, а также то, что границы его скрыты под газетой, кажется совершенно невозможным угадать, какие места на ковре будут внутренними по отношению к замкнутой кривой, обозначенной шнуром, а какие внешними. Тем не менее всякий раз показывающий может безошибочно установить, будет палец захвачен шнуром или нет.

Для другого варианта этой головоломки нужна дюжина или более простых булавок. Показывающий быстро и, как кажется, совсем наугад располагает их в различных местах видимой части узора, пока ими не будет утыкан весь прямоугольник. Затем шнур стягивается с ковра и все булавки остаются свободными. Можно взять одну булавку, отличающуюся по своему цвету (или размеру) от остальных, и поместить ее на узоре так, что после стягивания шнура с ковра она останется единственной захваченной в петлю, в то время как все остальные будут свободны. Можно предложить еще один вариант, когда все булавки размещаются внутри замкнутой кривой. В этом случае стягиваемый шнур образует петлю, окружающую все булавки.

Все эти головоломки основаны на нескольких простых правилах. Если какие-нибудь две точки лежат внутри кривой, образуемой шнуром, то соединяющая их воображаемая линия пересекает эту кривую четное число раз. То же самое справедливо и в случае, когда обе точки лежат вне кривой. Но если одна точка лежит внутри, а другая вне кривой, то соединительная линия всегда дает нечетное число пересечений.

Перед тем как будут положены газеты, выделите мысленно на узоре вблизи его середины какую-нибудь точку, внешнюю по отношению к кривой. Это нетрудно сделать, проведя, например, воображаемую линию от какой-нибудь точки вне узора по направлению к середине.

Вы можете, например, запомнить точку А на рис. 27.

Теперь, даже при закрытых газетами границах узора, для вас не составит труда определить, будет интересующая вас точка внутренней или внешней.

Для этого нужно лишь провести воображаемую линию (она не обязательно должна быть прямой, хотя, конечно, прямую линию представить легче всего) от требуемого места к точке, о которой вы знаете, что она внешняя, и заметить, будет число пересечений четным или нечетным.

Метод демонстрации всех вариантов, описанных выше, прост. Дюжину булавок можно быстро разместить вне замкнутой кривой следующим образом.

Первую булавку воткните в заранее известное место, затем дважды пересеките кривую и воткните следующую, еще раз дважды пересеките кривую и воткните третью булавку и т. д. Если же вы захотите захватить какую-нибудь одну отмеченную булавку, то, прежде чем воткнуть ее в ковер, пересеките кривую один раз, отправляясь от любой уже воткнутой булавки. Конечно, вы можете с такой же быстротой воткнуть все булавки и внутри замкнутой кривой.

Аналогичный фокус можно показать с карандашом и бумагой. Попросите кого-нибудь начертить на бумаге сколь угодно сложную замкнутую кривую (конечно, без самопересечений) и отогнуть назад все четыре стороны листа так, чтобы осталась видимой только внутренняя прямоугольная часть (рис. 28).

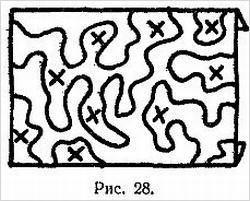
Пусть зритель, далее, поставит на узоре несколько крестиков. Вы берете карандаш и, не задумываясь, обводите ряд крестиков, говоря, что все они лежат внутри кривой. После этого стороны листа отгибаются обратно и все могут проверить, что вы не ошиблись.

Существует еще одна категория топологических головоломок со шнурами: все они начинаются со связывания кистей рук одним куском шнура (рис. 29).

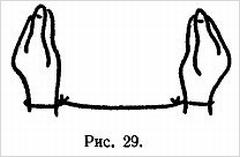
Можно, например, проделать со шнуром такие манипуляции, что на нем появится узел; он может быть обыкновенным или типа восьмерки. Можно надеть на шнур резиновое кольцо, а затем снять его со шнура, не развязывая н не разрывая при этом шнура.

Если два человека соединены зацепленными шнурами, как это показано на рис. 30, то можно манипулировать со шнурами так, чтобы освободить их от связки.

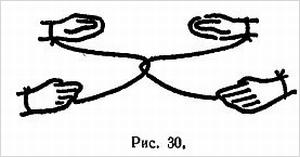
Решение всех перечисленных головоломок основано на том, что кольцо, образованное шнуром, руками и корпусом зрителя, на самом деле не сплошное, а имеет на кистях разрывы. Чтобы завязать на шнуре узел, нужно проделать следующее: образовать на нем петлю, пропустить ее изнутри под кольцо, завязанное на кисти, перекрутить один раз (т. е. на 180°) и протащить над рукой обратно, пропустить снаружи под кольцо и протащить над рукой вперед. При этом образуется обыкновенный узел. Узел в виде восьмерки получится точно таким же путем, но петлю нужно перекрутить дважды (на 360°). Резиновое кольцо надевают на шнур следующим образом: его натягивают на запястье и сдвигают немного далее на кисть, пропуская под веревочным кольцом, а затем перетягивают через руку и опускают на шнур. Производя эти манипуляции в обратном порядке, можно, конечно, снять кольцо. Два зрителя, связанных друг с другом так, как это было описано выше, освобождаются так: середина шнура, которым связаны руки одного зрителя, пропускается изнутри под кольцо, образованное шнуром на запястье другого зрителя, перетягивается через руку, а затем пропускается обратно под кольцом.

Очень старый фокус с тремя бусинами, нанизанными на две сложенные вместе нитки, известен под названием «бабушкиного ожерелья». (Идея этого фокуса используется также во многих других фокусах с лентами и шнурами.) Фокус начинают с демонстрации бусин, нанизанных на две сложенные вместе нити. Затем, когда зритель потянет за концы, бусины падают с нитей в руки показывающему.

На рис. 31 показано в разрезе, как должны нанизываться бусины. Хотя и кажется, что обе нити продеты сквозь все три бусины, в действительности же каждая из нитей «возвращается обратно», складываясь сама с собой.

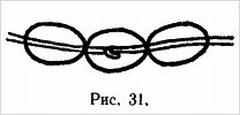
Концы нитей скрещиваются, как показано на рис. 32.

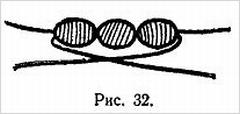
Если теперь потянуть за них (рис. 33), бусины спадут с нитей.

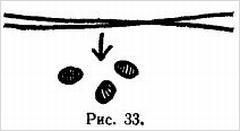
С топологией связано много методов разрезывания и «склеивания» шнуров, а также ряд остроумных способов завязывания и развязывания узлов на шнурах, концы которых во время демонстрации держат зажатыми.

Типичным узлом среди многих любопытных ложных узлов является следующий. Его начинают завязывать как обыкновенный двойной узел (рис. 34), а затем продевают один из концов шнура в нижнее, а затем в верхнее кольцо, как показано на рис. 35.

Если теперь потянуть за концы, узел сразу развяжется.

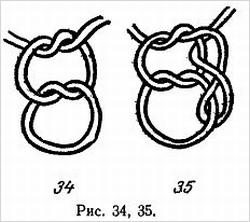
Три занимательных фокуса топологического характера для небольшой аудитории можно показать, пользуясь костюмными жилетами. С точки зрения топологии жилет можно рассматривать как двустороннюю поверхность с тремя не сцепленными краями, каждый из которых является обыкновенной замкнутой кривой. Застегнутый жилет является двусторонней поверхностью с четырьмя краями.

Зрителя, носящего жилет, просят снять пиджак.

Ему надевают на руку петлю, а затем просят заложить большой палец в нижний карман жилета, как показано на рис. 36.

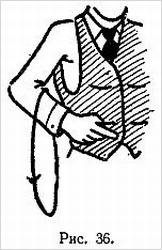
Теперь можно предложить присутствующим снять петлю с руки, не трогая большого пальца зрителя с места. Разгадка такова: петлю нужно протащить в жилетное отверстие для рукава, перебросить через голову зрителя, вытащить через второе отверстие для рукава и перенести под вторую руку. В результате этих действий петля окажется под жилетом, окружая собой грудь.

Опускайте ее, пока она не покажется из-под жилета, а затем дайте упасть на пол.

Зритель, носящий жилет, снимает пиджак и, соединив пальцы, вытягивает руки вперед. Можно ли вывернуть жилет наизнанку, не разнимая зрителю пальцев? Оказывается, можно. Для этого нужно расстегнуть жилет, поднять его над головой так, чтобы он повис на руках, вывернуть там наизнанку, просовывая через одно из отверстий для рукавов, и, наконец, надеть снова. Поразительно, что то же самое можно проделать и не расстегивая жилета, причем единственное затруднение будет в том, что застегнутый жилет слишком узок, чтобы его можно было стащить через голову. Однако этот фокус легко демонстрировать, заменив жилет свитером. Манипуляции со свитером должны быть точно такими же, как и с жилетом. Нетрудно демонстрировать этот фокус и на самом себе, для чего нужно соединить шнуром кисти рук, оставляя между ними сантиметров 50, чтобы обеспечить свободу движений. Вы сами можете убедиться, что стянуть свитер через голову, вывернуть его наизнанку через один из рукавов и снова надеть на себя совсем нетрудно.

Можно вывернуть жилет наизнанку со связанными руками, даже не снимая предварительно пиджака. Для этого нужно поднять пиджак кверху, пронести его над головой и оставить повисшим на руках. Затем поднять над головой жилет, через одно из его рукавных отверстий пропустить пиджак и вывернуть жилет наизнанку так, как это описывалось выше.

Оказывается, что жилет можно снять, не снимая пиджака. Проще всего это сделать так. Расстегнув сначала жилет, заложите левую полу пиджака зрителя на левое рукавное отверстие жилета с внешней стороны. Переведите затем это отверстие назад через левое плечо зрителя и далее вниз по его левой руке.

Теперь отверстие охватывает пиджак за левым плечом. Продолжайте передвигать отверстие по пиджаку дальше вокруг корпуса, переведите его через правое плечо и руку и, наконец, пропустите сквозь него правую половину пиджака. Таким образом, рукавное отверстие совершило почти полный оборот вокруг корпуса.

Жилет теперь висит под пиджаком на правом плече. Спустите его наполовину вниз сквозь правый рукав пиджака. Подверните обшлаг, захватите из-под него жилет и вытяните сквозь рукав наружу.

Вот два фокуса топологического характера с резиновыми кольцами.

Повесьте резиновое кольцо на свой указательный палец (рис. 37).

Заведите вторую половину кольца за средний палец (рис. 38) и зацепите снова за указательный, как показано на рис. 39.

Убедитесь в том, что кольцо охватывает пальцы точно так, как на рисунке. Попросите кого-нибудь взяться за кончик указательного пальца. Теперь согните средний палец, как на рис. 40. Если кольцо было надето правильно, то часть его соскользнет с конца среднего пальца.

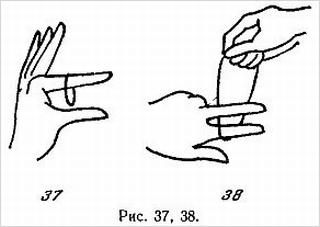
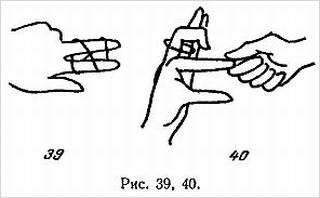
Вследствие этого и все кольцо свободно соскочит с указательного пальца и повиснет на среднем, как это показано на рис. 40.

Для показа другого фокуса нужно широкое резиновое кольцо, которое вначале держится, как показано на рис. 41.

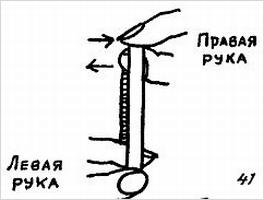
Затем оно дважды перекручивается; делается это при помощи большого и указательного пальцев, которые нужно двигать в направлениях, показанных на рис. 42 стрелками.

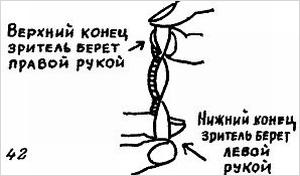
Попросите кого-нибудь снять с вашего пальца кольцо, захватив его точно таким же образом, как держали вы, т. е. так, чтобы правые большой и указательный пальцы удерживали кольцо за верхний конец, тогда как левые большой и указательный пальцы за нижний. Теперь предложите распрямить кольцо (т. е. избавиться от перекручиваний), меняя положение рук, но, конечно, не разжимая при этом пальцев.

Сколько бы зритель ни двигал руками, в конце концов, он должен будет признать, что не может этого сделать. Тогда вы аккуратно снимаете кольцо с его рук, взяв его точно так же, как держали первоначально. Затем очень медленно опускаете правую руку и поднимаете левую, как это показано на рис. 43. Когда вы это делаете, перекручивания чудесным образом исчезают на глазах.

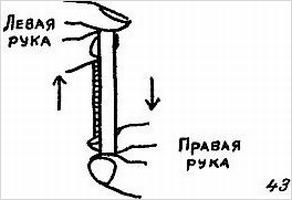
Секрет этого фокуса можно объяснить топологически. Перекрученное кольцо вместе с вашими руками и телом образуют некоторую топологическую структуру. Когда кольцо берет зритель, получается «левый вариант» этой структуры, топологически существенно отличный от вашего. В этом случае от перекручивания избавиться невозможно.

---

Среди фокусов, требующих специального снаряжения, очень немногие имеют математический характер. Мы выберем из них несколько наиболее интересных и таких, для которых читатель сможет собственноручно изготовить приспособления.

Я не знаю, когда появилось первое специальное приспособление математического характера, предназначенное для демонстрации фокуса, или каким оно было, но кажется несомненным, что одним из самых старых фокусов, в котором оно могло потребоваться, был фокус с узнаванием возраста лица или задуманного им числа при помощи серии карточек с числами.

Простейший вариант этого фокуса показывается при помощи серии карточек (обычно их бывает шесть или больше), на каждой из которых имеется ряд чисел. Зритель просматривает все карточки и передает фокуснику те из них, на которых имеется задуманное им число. Взглянув на переданные ему карточки, фокусник может сразу назвать это число. Для этого ему нужно только сложить наименьшие («ключевые») числа, соответствующие каждой карточке. Так как числа на карточках обычно располагаются в порядке возрастания (это облегчает зрителю отыскивание задуманного им числа, если оно есть на данной карточке), то ключевые числа будут сразу видны. Первым ключевым числом обычно берется 1, а остальные получаются путем удваивания предыдущего числа. Так, при шести карточках это будут числа 1, 2, 4, 8, 16 и 32 [21]). С их помощью, комбинируя различным образом карточки, можно получить суммы от 1 до 63.

Иногда карточки раскрашиваются в различные цвета.

Это дает возможность показывающему (который должен запомнить ключевое число, соответствующее каждому цвету) отходить в сторону, когда зритель сортирует карты, и называть задуманное число, не глядя на лицевую сторону карточек.

В несколько более сложном варианте только что рассмотренного фокуса для получения ключевых чисел применяется специальное перфорирование карточки.

После того как зритель отберет все карточки, на которых имеется задуманное число, показывающий кладет их друг на друга и накрывает «волшебной» карточкой (рис. 44).

Теперь, чтобы получить задуманное число, нужно сложить числа, видимые сквозь отверстия.

В принципе эта серия карточек не отличается от серии карточек с ключевыми числами. Однако числа на перфокартах не расположены в порядке возрастания, так что ключевые числа (т. е. числа, каждое из которых меньше всех остальных на данной карточке) занимают различные положения среди остальных чисел. Отверстия в «волшебной» карточке соответствуют местам, где на шести карточках расположены ключевые числа, а на каждой из шести карточек отверстия сделаны в тех же местах, что и на «магической» карточке, за исключением одного, где проставлено ключевое число данной карточки.

Вот фокус, в котором прикосновения к предметам сопровождаются побуквенным произношением чисел.

Показывается он на шести небольших, раскрашенных в различные цвета, квадратных пластинках, на каждой из которых изображено число (рис. 45).

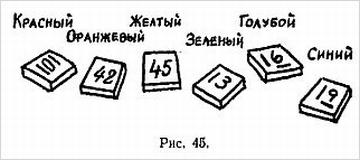
Пластинки раскладываются на столе числами вниз.

Показывающий отворачивается, а зритель в это время приподнимает одну пластинку, смотрит на число, а затем смешивает ее с остальными. Теперь показывающий поворачивается к столу и начинает притрагиваться карандашом к пластинкам. Зритель же в это время произносит про себя побуквенно свое число так, чтобы на каждое прикосновение приходилось по одной букве. Когда все буквы замеченного числа будут исчерпаны, он произносит: «стоп». Пластинка, на которой остановился карандаш, переворачивается, причем оказывается, что на ней как раз и есть задуманное число.

Объяснение. Первые шесть прикосновений делаются в произвольном порядке. Следующие шесть — в такой последовательности: 101, 42, 45, 13, 16, 19.

Показывающему нетрудно будет выдержать этот порядок, запомнив соответствующую последовательность цветов. Конечно, этот фокус получается благодаря тому, что запись числа 101 (сто один) содержит семь букв, а запись каждого из следующих чисел — одной буквой больше [22]). Читатель без труда может изготовить серию таких пластинок из картона или пластмассы.

Существует много и других фокусов, в которых применяется принцип побуквенного произношения слов. Такова, например, «карта цветов». Лицевая ее сторона представлена на рис. 46.

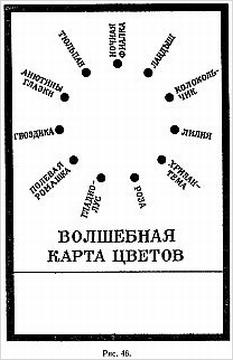
Зритель задумывает цветок, и показывающий начинает перебирать карандашом отверстия. При каждом прикосновении зритель называет про себя одну букву из названия выбранного цветка и произносит вслух: «стоп», когда его слово будет исчерпано. Карандаш вставляется в последнее затронутое отверстие, и карта переворачивается. Острие его будет высовываться как раз там, где напечатано название задуманного цветка.

Первое прикосновение делается у верхнего отверстия, далее отверстия обходятся через одно по часовой стрелке.

Фокус-картинка, похожая на только что описанную «карту цветов», изображена на рис. 47.

Зритель задумывает какое-нибудь животное, изображенное на рисунке, и произносит про себя название его по буквам, в то время как показывающий дотрагивается до рисунков.

Начав с жеребенка, он переходит затем вверх по линии к гиппопотаму и так продолжает обход всех животных, двигаясь в направлениях, указываемых линиями, пока зритель не дойдет до последней буквы своего слова и не скажет «стоп».

Для показа этого фокуса берутся пять игральных костей, на гранях которых изображены различные трехзначные числа, всего 30 чисел. Зритель бросает кости на стол, и показывающий тут же объявляет сумму пяти выпавших чисел.

Чтобы получить эту сумму, показывающий складывает последние цифры всех этих чисел и вычитает полученное число из 50. Поставив найденную разность перед вычитаемым, он получает четырехзначное число, которое и будет искомой суммой пяти трехзначных чисел, выпавших на костях. Допустим, например, что сумма последних цифр равна 26. Вычитая 26 из 50, получаем 24; в ответе будет число 2426.

Наши пять костей несут на себе следующие числа:

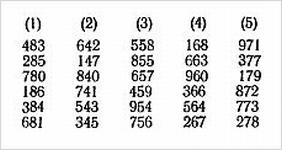
Вот один интересный вариант фокуса с домино, объясненного во второй главе. Десять костей для игры в домино кладутся в узкий пластмассовый ящичек, открывающийся сверху (рис. 48).

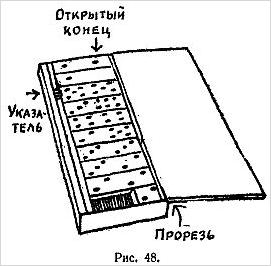
Справа в ящичке отверстие, сквозь которое можно выдвинуть нижнюю косточку наружу, и второе отверстие сверху, сквозь которое ее можно вставить обратно в ящичек при закрытой крышке. К левой планке ящичка прикреплен указатель, который можно двигать вверх и вниз. Показывающий устанавливает указатель, закрывает крышку и предлагает зрителю сдвинуть несколько косточек (от 1 до 10) снизу вверх. Допустим, что он передвинул 6 косточек. После того как крышка будет открыта, выясняется, что против указателя стоит косточка, на которой сумма очков равна шести. Фокус можно тут же повторить, не меняя положения косточек.

Перед демонстрацией этого фокуса показывающий должен установить указатель против косточки, на которой сумма очков равна 10, после чего фокус получается автоматически. Такой ящичек не представляет труда сделать самому.

Для демонстрации нужно иметь 6 фишек, на обеих сторонах которых имеются числа. На верхней части рис. 49 показана одна сторона фишек, на нижней части — соответствующая им обратная сторона. Обратим внимание на то, что цифры верхнего ряда выписаны жирными линиями; в нижнем же ряду цифры более тонкие.

Показывающий просит зрителя перемешать фишки между ладонями, а затем разложить их на столе в два ряда по три фишки в каждом. Пока показывающий стоит, повернувшись спиной, зритель переворачивает три фишки, не сообщая при этом, какие именно. Затем показывающий просит перевернуть еще несколько фишек. После этого зритель берет любую фишку по своему желанию, переворачивает ее и чем-нибудь накрывает (например, игральной картой или монетой — лишь бы не была видна цифра).

То же самое он повторяет еще с двумя фишками.

Теперь на столе три фишки открыты, а три закрыты.

В этот момент показывающий поворачивается к зрителям и называет сумму трех накрытых чисел.

Сущность фокуса состоит в следующем. Прежде чем отвернуться от стола, фокусник бросает беглый взгляд на фишки и запоминает местоположение тех, которые обращены жирными цифрами кверху. После того как зритель перевернет три произвольные фишки, показывающий просит его перевернуть еще несколько фишек.

Он говорит: «Переверните, пожалуйста, вторую фишку в первом ряду и третью фишку в нижнем ряду». Эти фишки должны быть те самые, положение которых он запомнил (т. е. которые вначале находились на местах, занятых фишками, обращенными жирными числами кверху).

Теперь зритель переворачивает три фишки, накрывая каждую из них картой. Показывающий поворачивается к зрителям и производит в уме следующие вычисления: он замечает число фишек, обращенных жирными числами кверху (оно будет равно нулю, одному, двум или трем), и умножает это число на 10. К полученному произведению прибавляет 15. Из этой суммы отнимает сумму трех открытых чисел. Остаток будет равен сумме верхних чисел на трех фишках, накрытых картами [23]).

---

В этой и следующей главах мы проследим за ходом развития многих замечательных геометрических парадоксов. Все они начинаются с разрезания фигуры на куски и заканчиваются составлением из этих кусков новой фигуры. При этом создается впечатление, что часть первоначальной фигуры (это может быть часть площади фигуры или один из нескольких изображенных на ней рисунков) бесследно исчезла. Когда же куски возвращаются на свои первоначальные места, исчезнувшая часть площади или рисунок таинственным образом возникают вновь.

Геометрический характер этих любопытных исчезновений и появлений оправдывает причисление этих парадоксов к разряду математических головоломок.

Все многочисленные парадоксы, которые мы здесь собираемся рассматривать, основаны на одном и том же принципе, который мы назовем «принципом скрытого перераспределения». Вот один очень старый и совсем элементарный парадокс, который сразу объясняет суть этого принципа.

Начертим на прямоугольном листе бумаги десять вертикальных линий одинаковой длины и проведем пунктиром диагональ, как показано на рис. 50.

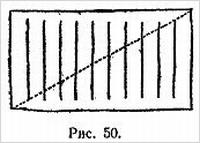
Посмотрим на отрезки этих линий над диагональю и под ней; нетрудно заметить, что длина первых уменьшается, а вторых соответственно увеличивается.

Разрежем прямоугольник по пунктирной линии и сдвинем нижнюю часть влево вниз, как это показано на рис. 51.

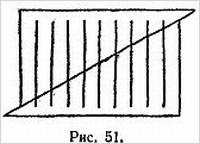
Сосчитав число вертикальных линий, вы обнаружите, что теперь их стало девять. Какая линия исчезла и куда? Передвиньте левую часть в прежнее положение, и исчезнувшая линия появится снова.

Но какая линия стала на свое место и откуда она взялась?

Сначала эти вопросы кажутся загадочными, но после небольшого размышления становится ясным, что никакая отдельная линия при этом не исчезает и не появляется. Происходит же следующее: восемь этих приращений в точности равна длине каждой из первоначальных линий.

Возможно, суть парадокса выступит еще более явственно, если его иллюстрировать на камешках.

Возьмем пять кучек камешков по четыре камешка в кучке. Переместим один камешек из второй кучки в первую, два камешка из третьей во вторую, три из четвертой в третью и, наконец, все четыре камешка из пятой в четвертую. Рис. 52 поясняет наши действия.

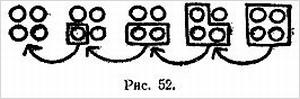
После такой передвижки оказывается, что кучек стало только четыре. Невозможно ответить на вопрос, какая кучка исчезла, так как камешки были перераспределены так, что в каждой из четырех кучек прибавилось по камешку. В точности то же происходит и в парадоксе с линиями. Когда части листа сдвигаются по диагонали, отрезки разрезанных линий перераспределяются и каждая получающаяся при этом линия становится немного длиннее первоначальной.

Перейдем к описанию способов, при помощи которых парадокс с линиями можно сделать более интересным и занимательным. Этого можно, например, достигнуть, заменив исчезновение и появление линий таким же исчезновением и появлением плоских фигур. Здесь особенно подойдут изображения карандашей, папирос, кирпичей, шляп с высокой тульей, стаканов с водой и других вертикально протяженных предметов, характер изображения которых до и после сдвига остается одинаковым. При некоторой художественной изобретательности можно брать и более сложные предметы. Посмотрите, например, на исчезающее лицо на рис. 53.

При сдвиге нижней полосы на верхней части рисунка влево все шляпы остаются незатронутыми, однако одно лицо полностью исчезает! (см. нижнюю часть рисунка). Бессмысленно спрашивать, какое именно лицо, так как при сдвиге четыре лица разделяются на две части. Эти части затем перераспределяются, причем каждое лицо получает несколько добавочных черт: одно, например, более длинный нос, другое — более вытянутый подбородок и т. д. Однако эти маленькие перераспределения остроумно скрыты, а исчезновение всего лица, конечно, поражает гораздо сильнее, чем исчезновение кусочка линии.

В этой головоломке парадоксу с линиями придана круговая форма и прямолинейные отрезки заменены фигурами 13 воинов (рис. 54).

Большая стрела указывает при этом на северо-восток С. В. Если же рисунок разрезать по окружности, а затем внутреннюю часть начать поворачивать против часовой стрелки, то фигуры сначала разделятся на части, затем соединятся вновь, но уже по-иному, и когда большая стрела укажет на северо-запад С.З., на рисунке будет 12 воинов (рис. 55).

При вращении круга в обратном направлении до положения, когда большая стрела встанет опять на СВ., исчезнувший воин появится снова.

Если рис. 54 рассмотреть повнимательнее, то можно заметить, что два воина в левой нижней части рисунка расположены по-особенному: они находятся друг против друга, тогда как все остальные размещены цепочкой. Эти две фигуры соответствуют крайним линиям в парадоксе с отрезками. Исходя из требований рисунка, у каждой из этих фигур должна отсутствовать часть ноги, и чтобы в повернутом положении колеса этот недостаток был менее заметен, лучше было изобразить их рядом.

Вращая колесо далее, можно получить четырнадцать, пятнадцать и т. д. воинов, однако с увеличением их числа становится все более явственным, что каждая из фигур сильно тощает, давая материал для других фигур.

Отметим еще, что воины изображены на рисунке с гораздо большей изобретательностью, чем это может показаться с первого взгляда. Так, например, чтобы фигуры оставались в вертикальном положении во всех местах глобуса, нужно в одном случае иметь вместо левой ноги правую, а в другом, наоборот, вместо правой ноги левую.

Парадокс вертикальных линий можно, очевидно, показывать и на более сложных объектах, например человеческих лицах, фигурах животных и т. д. На рис. 56 показан один вариант.

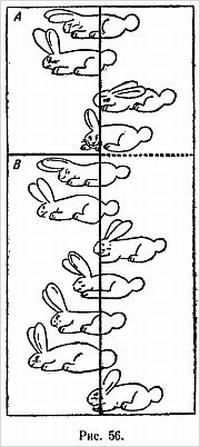
Когда после разрезании по толстой линии меняют местами прямоугольники А а В, один кролик исчезает, оставляя вместо себя пасхальное яйцо. Если вместо перестановки прямоугольников А и В разрезать правую половину рисунка по пунктирной линии и поменять местами правые части, число кроликов увеличится до 12, однако при этом один кролик теряет уши и появляются другие смешные детали.

В близкой связи с парадоксами, рассмотренными в предыдущей главе, находится другой класс парадоксов, в котором «принципом скрытого перераспределения» объясняется таинственное исчезновение или появление площадей. Один из самых старых и самых простых примеров парадоксов этого рода приведен на рис. 57.

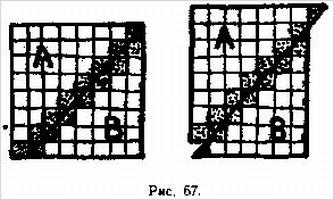
Шахматная доска разрезается наискось, как это изображено на левой половине рисунка, а затем часть В сдвигается влево вниз, как это показано на правой половине рисунка. Если треугольник, выступающий в правом верхнем углу, отрезать ножницами и поместить на свободное место, имеющее вид треугольника в левом нижнем углу рисунка, то получится прямоугольник в 7×9 квадратных единиц.

Первоначальная площадь равнялась 64 квадратным единицам, теперь же она равна 63. Куда исчезла одна недостающая квадратная единица?

Ответ состоит в том, что наша диагональная линия проходит несколько ниже левого нижнего угла клетки, находящейся в правом верхнем углу доски.

Благодаря этому отрезанный треугольник имеет высоту, равную не 1, а 1 1/7. И, таким образом, высота равна не 9, а 9 1/7 единицам. Увеличение высоты на 1/7 единицы почти незаметно, но, будучи принято в расчет, оно приводит к требуемой площади прямоугольника в 64 квадратные единицы.

Парадокс становится еще более поразительным, если вместо шахматной доски взять просто квадратный лист бумаги без клеток, так как в нашем случае при внимательном изучении обнаруживается неаккуратное смыкание клеток вдоль линии разреза.

Связь нашего парадокса с парадоксом вертикальных линий, рассмотренным в предыдущей главе, становится ясной, если проследить за клетками у линии разреза. При продвижении вдоль линии разреза вверх обнаруживается, что над линией части разрезанных клеток (на рисунке они затемнены) постепенно уменьшаются, а под линией постепенно увеличиваются. На шахматной доске было пятнадцать затемненных клеток, а на прямоугольнике, получившемся после перестановки частей, их стало только четырнадцать. Кажущееся исчезновение одной затемненной клетки есть просто другая форма рассмотренного выше парадокса. Когда мы отрезаем и затем перемешаем маленький треугольничек, мы фактически разрезаем часть А шахматной доски на два куска, которые затем меняются местами вдоль диагонали.

Для головоломки важны только клетки, прилежащие к линии разреза, остальные же никакого значения не имеют, играя роль оформления. Однако присутствие их меняет характер парадокса. Вместо исчезновения одной из нескольких маленьких клеток (или несколько более сложной фигуры, скажем, игральной карты, человеческого лица и т. п., которую можно было начертить внутри каждой клетки) мы сталкиваемся здесь с изменением площади большой геометрической фигуры.

Вот еще один парадокс с площадью. Меняя положение частей А и С, как показано на рис. 58, можно превратить прямоугольник площадью в 30 квадратных единиц в два меньших прямоугольника с общей площадью в 32 квадратные единицы, получая, таким образом, «выигрыш» в две квадратные единицы. Как и в предыдущем парадоксе, здесь играют роль только клетки, примыкающие к линии разреза. Остальные нужны лишь как оформление.

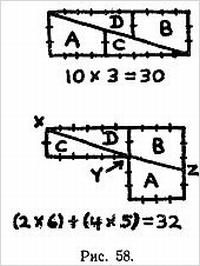
В этом парадоксе существуют два существенно различных способа разрезывания фигуры на части.

Можно начать с большого прямоугольника размером 3×10 единиц (верхняя часть рис. 58), аккуратно проводя в нем диагональ, тогда два меньших прямоугольника (нижняя часть рис. 58) будут на 1/5 единицы короче своих кажущихся размеров.

Но можно также начать с фигуры, составленной из двух аккуратно начерченных меньших прямоугольников размером 2×6 и 4×5 единиц; тогда отрезки, соединяющие точку X с точкой У и точку У с точкой Z, не будут составлять прямую линию. И только потому, что образуемый ими тупой угол с вершиной в точке У весьма близок к развернутому, ломаная ХУZ кажется прямой линией. Поэтому фигура, составленная из частей малых прямоугольников, не будет в действительности прямоугольником, так как эти части будут слегка перекрываться вдоль диагонали. Парадокс с шахматной доской, так же как и большая часть других парадоксов, которые мы собираемся рассмотреть в этой главе, тоже могут быть представлены в двух вариантах. В одном из них парадокс получается за счет незначительного уменьшения или увеличения высоты (или ширины) фигур, в другом — за счет прироста или потери площади вдоль диагонали, вызываемых либо перекрыванием фигур, как в только что рассмотренном случае, либо появлением пустых мест, с чем мы вскоре встретимся.

Меняя размеры фигур и наклон диагонали, этому парадоксу можно придать самое различное оформление. Можно добиться потери или прироста площади в 1 квадратную единицу или в 2, 3, 4, 5 единиц и т. д.

Конечно, чем дальше вы зайдете, тем легче будет обнаружить, куда деваются недостающие квадраты.

В одном изящном варианте исходные прямоугольники размером 3×8 и 5×8 единиц, будучи приставлены друг к другу, образуют обычную шахматную доску в 8х8 клеток. Эти прямоугольники разрезаются на части, которые после перераспределения образуют новый большой прямоугольник с кажущимся приростом площади в одну квадратную единицу (рис. 59).

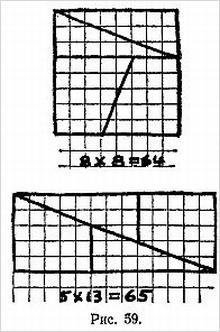
Суть парадокса состоит в следующем. При аккуратном построении чертежа квадрата строгой диагонали большого прямоугольника не получается. Вместо нее появляется ромбовидная фигура, настолько вытянутая что стороны ее кажутся почти слившимися. С другой стороны, при аккуратном проведении диагонали большого прямоугольник; высота верхнего из двух прямоугольников, составляющих квадрат, будет чуть больше, чем это должно быть, а нижний прямоугольник — чуть шире. Заметим, что неаккуратное смыкание частей фигуры при втором способе разрезывания больше бросается в глаза, чем неточности вдоль диагонали в первом; поэтому первый способ предпочтительнее. Как и в ранее встречавшихся примерах, внутри клеток, рассеченных диагональю, можно рисовать кружочки, физиономии или какие-нибудь фигурки; при перестановке составных частей прямоугольников этих фигурок будет становиться одной больше или меньше.

Оказывается, что длины сторон четырех частей, составляющих фигуры (рис. 59 и 60), являются членами ряда Фибоначчи, т. е. ряда чисел, начинающегося с двух единиц: 1, 1, каждое из которых, начиная с третьего, есть сумма двух предшествующих. Наш ряд имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34…

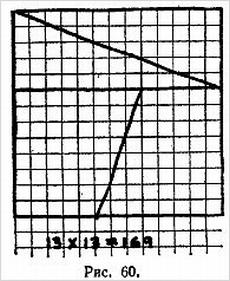
Расположение частей, иа которые был разрезан квадрат, в виде прямоугольника иллюстрирует одно из свойств ряда Фибоначчи, а именно следующее: при возведении в квадрат любого члена этого ряда получается произведение двух соседних членов ряда плюс или минус единица. В нашем примере сторона квадрата равна 8, а площадь равна 64. Восьмерка в ряду Фибоначчи расположена между 5 и 13. Так как числа 5 и 13 становятся длинами сторон прямоугольника, то площадь его должна быть равной 65, что дает прирост площади в одну единицу.

Благодаря этому свойству ряда можно построить квадрат, стороной которого является любое число Фибоначчи, большее единицы, а затем разрезать его в соответствии с двумя предшествующими числами этого ряда.

Если, например, взять квадрат в 13×13 единиц, то три его стороны следует разделить на отрезки длиной в 5 и 8 единиц, а затем разрезать, как показано на рис. 60. Площадь этого квадрата равна 169 квадратным единицам. Стороны прямоугольника, образованного частями квадратов, будут 21 и 8, что дает площадь в 168 квадратных единиц. Здесь благодаря перекрыванию частей вдоль диагонали одна квадратная единица не прибавляется, а теряется.

Если взять квадрат со стороной 5, то тоже произойдет потеря одной квадратной единицы. Можно сформулировать и общее правило: приняв за сторону квадрата какое-нибудь число из «первой» подпоследовательности расположенных через одно чисел Фибоначчи (3, 8…) и составив из частей этого квадрата прямоугольник, мы получим вдоль его диагонали просвет и как следствие кажущийся прирост площади на одну единицу. Взяв же за сторону квадрата какое-нибудь число из «второй» подпоследовательности (2, 5, 13…), мы получим вдоль диагонали прямоугольника перекрывание площадей и потерю одной квадратной единицы площади.

Чем дальше мы продвигаемся по ряду чисел Фибоначчи, тем менее заметными становятся перекрывания или просветы. И наоборот, чем ниже мы спускаемся по ряду, тем они становятся более существенными.

Можно построить парадокс даже на квадрате со стороной в две единицы. Но тогда в прямоугольнике 3×1 получается столь очевидное перекрывание, что эффект парадокса полностью теряется.

Используя для парадокса другие ряды Фибоначчи, можно получить бесчисленное множество вариантов. Так, например, квадраты, основанные на ряде 2, 4, 6, 10, 16, 26 и т. д., приводят к потерям или приростам площади в 4 квадратные единицы. Величину этих потерь или приростов можно узнать, вычисляя для данного ряда разности между квадратом любого его члена и произведением двух его соседних членов слева и справа. Ряд 3, 4, 7, 11, 18, 29 и т. д. дает прирост или потерю в пять квадратных единиц. Т. де Мулидар привел рисунок квадрата, основанного на ряде 1, 4, 5, 9, 14 и т. д. Сторона этого квадрата взята равной 9, и после преобразования его в прямоугольник теряется 11 квадратных единиц. Ряд 2, 5, 7, 12, 19… также дает потерю или прирост в 11 квадратных единиц. В обоих случаях перекрывания (или просветы) вдоль диагонали оказываются настолько большими, что их сразу можно заметить.

Обозначив какие-нибудь три последовательных числа Фибоначчи через А, В и С, а через X — потерю или прирост площади, мы получим следующие две формулы:

А + В = С

В² = АС ± Х

Если подставить вместо X желаемый прирост или потерю, а вместо В число, которое принято за длину стороны квадрата, то можно построить квадратное уравнение, из которого найдутся два других числа Фибоначчи, хотя это, конечно, не обязательно будут рациональные числа. Оказывается, например, что, деля квадрат на фигуры с рациональными длинами сторон, нельзя получить прирост или потерю в две или три квадратные единицы. С помощью иррациональных чисел это, конечно, можно достигнуть. Так, ряд Фибоначчи 2^1/2, 2·2^1/2, 3·2^1/2, 5·2^1/2 дает прирост или потерю в две квадратные единицы, а ряд 3^1/2, 2·3^1/2, 3·3^1/2, 5·3^1/2 приводит к приросту или потере в три квадратные единицы.

Существует много способов, которыми прямоугольник можно разрезать на небольшое число частей, а затем сложить их в виде другого прямоугольника большей или меньшей площади. На рис. 61 изображен парадокс, также основанный на ряде Фибоначчи.

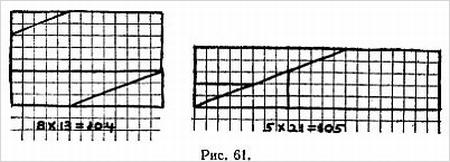
Подобно только что рассмотренному случаю с квадратом, выбор какого-нибудь числа Фибоначчи из «второй» подпоследовательности в качестве ширины первого прямоугольника (в рассматриваемом случае 13) приводит к увеличению площади второго прямоугольника на одну квадратную единицу.

Если же за ширину первого прямоугольника принять какое-нибудь число Фибоначчи из «дополнительной» подпоследовательности, то во втором прямоугольнике площадь уменьшится на одну единицу. Потери и приросты площади объясняются небольшими перекрываниями или просветами вдоль диагонального разреза второго прямоугольника. Другой вариант такого прямоугольника, показанный на рис. 62, при построении второго прямоугольника приводит к увеличению площади на две квадратные единицы.

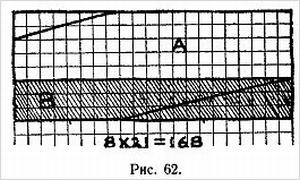
Если заштрихованную часть площяди второго прямоугольника поместить над незаштрихованной частью, два диагональных разреза сольются в одну большую диагональ. Переставляя теперь части А и В (как на рис. 61), мы получим второй прямоугольник большей площади.

При суммировании площадей частей перестановка треугольников В и С в верхней части рис. 63 приводит к кажущейся потере одной квадратной единицы.

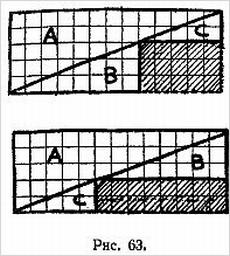
Как читатель заметит, это происходит за счет площадей заштрихованных частей: на верхней части рисунка имеется 15 заштрихованных квадратиков, на нижней — 16. Заменяя заштрихованные куски двумя покрывающими их фигурами специального вида, мы приходим к новой, поразительной форме парадокса. Теперь перед нами прямоугольник, который можно разрезать на 5 частей, а затем, меняя их местами, составить новый прямоугольник, причем, несмотря на то, что его линейные размеры остаются прежними, внутри появляется отверстие площадью в одну квадратную единицу (рис. 64).

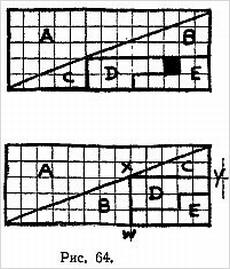
Возможность преобразования одной фигуры в другую, тех же внешних размеров, но с отверстием внутри периметра, основана на следующем. Если взять точку X точно в трех единицах от основания и в пяти единицах от боковой стороны прямоугольника, то диагональ через нее проходить не будет. Однако ломаная, соединяющая точку X с противоположными вершинами прямоугольника, будет так мало отклоняться от диагонали, что это будет почти незаметно.

После перестановки треугольников В и С на нижней половине рисунка части фигуры будут слегка перекрываться вдоль диагонали.

С другой стороны, если в верхней части рисунка рассматривать линию, соединяющую противоположные вершины прямоугольника, как точно проведенную диагональ, то линия XW будет чуть длиннее трех единиц. И как следствие этого второй прямоугольник будет несколько выше, чем кажется. В первом случае недостающую единицу площади можно считать распределенной с угла на угол и образующей перекрывание вдоль диагоналей. Во втором случае недостающий квадратик распределен по ширине прямоугольника. Как мы уже знаем из предыдущего, все парадоксы такого рода можно отнести к одному из этих двух вариантов построения. В обоих случаях неточности фигур настолько незначительны, что они оказываются совершенно незаметными.

Наиболее изящной формой этого парадокса являются квадраты, которые после перераспределения частей и образования отверстия остаются квадратами.

Такие квадраты известны в бесчисленных вариантах и с отверстиями в любое число квадратных единиц. Некоторые, наиболее интересные из них изображены на рис. 65 и 66.

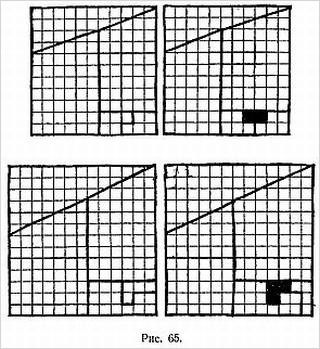
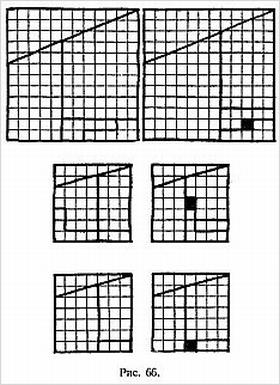
Можно указать на простую формулу, связывающую размер отверстия с пропорциями большого треугольника. Три размера, о которых пойдет речь, мы обозначим через А, В к С (рис. 67).

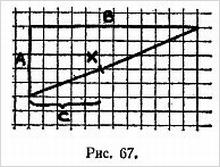
Площадь отверстия в квадратных единицах равна разности между произведением А на С и ближайшим к нему кратным размера В. Так, в последнем примере произведение А и С равно 25. Ближайшее кратное размера В к 25 есть 24, поэтому отверстие получается в одну квадратную единицу. Это правило действует независимо от того, проведена ли настоящая диагональ или же точка X на рис. 67 нанесена аккуратно на пересечении линий квадратной сетки.

Если диагональ, как это и должно быть, вычерчивается как строго прямая линия или если точка X берется точно в одной из вершин квадратной сетки, то никакого парадокса не получается. В этих случаях формула дает отверстие размером в нуль квадратных единиц, обозначая этим, конечно, что отверстия нет вообще.

Вернемся к первому примеру парадокса (см. рис. 64). Заметим, что большой треугольник А не меняет своего положения, в то время как остальные части перемещаются. Поскольку этот треугольник не играет существенной роли в парадоксе, его можно вообще отбросить, оставляя только правый треугольник, разрезанный на четыре части. Эти части можно затем перераспределить, получая при этом прямоугольный треугольник с отверстием (рис. 68), будто бы равный исходному.

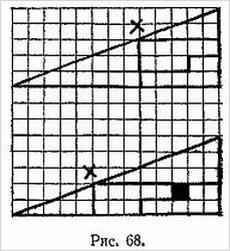
Составляя два таких прямоугольных треугольника катетами, можно построить много вариантов равнобедренных треугольников, подобных изображенному на рис. 69.

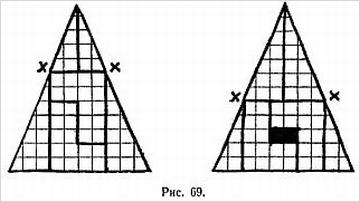
Так же как и в ранее рассмотренных парадоксах, эти треугольники можно строить двумя способами: либо проводить их боковые стороны строго прямолинейно, тогда точка X не попадет на пересечение линий квадратной сетки, либо помещать точку X точно в пересечение, тогда боковые стороны будут слегка выпуклыми или вогнутыми. Последний способ, кажется, лучше маскирует неточности чертежа. Парадокс покажется еще более удивительным, если на частях, составляющих треугольник, нанести линии квадратной сетки, подчеркивая этим самым, что части изготовлялись с необходимой аккуратностью.

Придавая нашим равнобедренным треугольникам различные размеры, можно добиться прироста или потери любого четного числа квадратных единиц.

Несколько типичных примеров дано на рис. 70, 71 и 72.

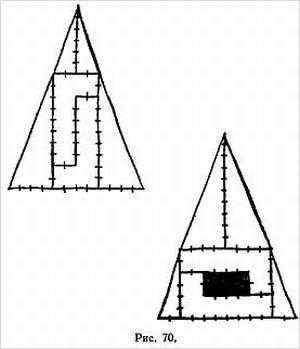
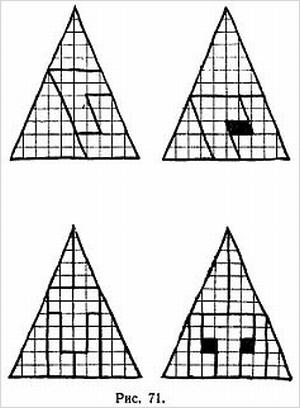
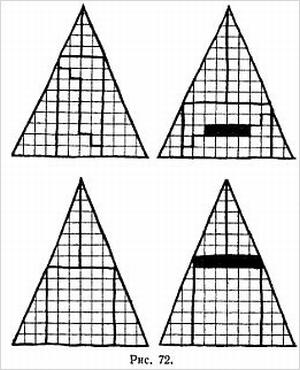
Составляя основаниями два равнобедренных треугольника любого из этих типов, можно построить самые различные варианты ромбического вида; однако они не добавят ничего существенно нового к нашему парадоксу.

Все рассмотренные нами до сих пор виды парадоксов с изменением площади близко связаны между собой по способу построения. Однако существуют парадоксы, полученные и совершенно отличными методами. Можно, например, разрезать квадрат на четыре части одинаковой формы и размера (рис. 73), а затем составить их по-новому так, как показано на рис. 74. При этом получается квадрат, размеры которого кажутся не изменившимися и в то же время с отверстием в середине.

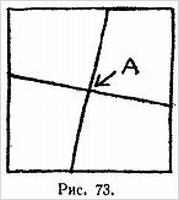
Подобным же образом можно разрезать прямоугольник с любым соотношением длин сторон. Любопытно, что точка А, в которой пересекаются две которого кажутся не изменившимися и в то же время с отверстием в середине.

Подобным же образом можно разрезать прямоугольник с любым соотношением длин сторон. Любопытно, что точка А, в которой пересекаются две взаимно перпендикулярные линии разреза, может при этом находиться в любом месте внутри прямоугольника. В каждом случае при перераспределении частей появляется отверстие, причем размер его зависит от величины угла, образованного линиями разреза со сторонами прямоугольника.

Этот парадокс отличается сравнительной простотой, однако он много теряет благодаря тому, что даже при поверхностном изучении видно, что стороны второго прямоугольника должны быть немного больше, чем стороны первого.

Более сложный способ разрезания квадрата на четыре части, при котором получается внутреннее отверстие, изображен на рис. 75.

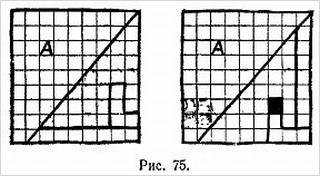
Он основан на парадоксе с шахматной доской, которым открывается настоящая глава. Заметим, что при перераспределении частей две из них нужно перевернуть обратной стороной кверху. Заметим также, что при отбрасывании части А мы получаем прямоугольный треугольник, составленный из трех частей, внутри которого можно образовать отверстие.

Существует ли способ разрезывания квадрата на три части, которые можно составить по-новому так, чтобы получился квадрат с отверстием внутри? Ответ будет положительным. Одно изящное решение основано на применении парадокса, рассмотренного в предыдущей главе.

Вместо того чтобы специальным образом располагать картинки уступами, а разрез производить прямолинейно (горизонтально), картинки размещают на одной прямой, а разрез делают уступами. Результат получается поразительный: не только пропадает картинка, но на месте ее исчезновения появляется отверстие.

Можно ли сделать то же самое при двух частях?

Я не думаю, что в этом случае можно каким-нибудь методом получить внутреннее отверстие в квадрате за счет незаметного увеличения его высоты или ширины. Однако было показано, что парадокс с отверстием в квадрате, разрезаемом на две части, можно построить на принципе, который применяется в парадоксе с исчезающим воином. В этом случае вместо размещения фигурок по спирали или ступенькой их размещают строго по окружности, тогда как разрез делают спиральным или ступенчатым; в последнем случае он имеет вид зубчатого колеса с зубцами различных размеров. При вращении этого колеса одна фигурка исчезает и вместо нее появляется отверстие.

Неподвижная и вращающиеся части аккуратно пригнаны друг к другу только в положении, когда появляется отверстие. В исходном же положении видны небольшие просветы у каждого зубца, если разрез был ступенчатым, или один непрерывный круговой просвет при разрезе, идущем по спирали.

Если исходный прямоугольник не является квадратом, его можно разрезать на две части, а затем получить внутри отверстие при совсем мало заметном изменении его внешних размеров. На рис. 76 показан один вариант.

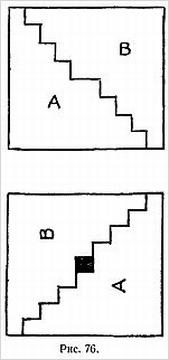
Обе части при этом тождественны как по форме, так и по размерам. Проще всего демонстрировать этот парадокс следующим образом: вырезать части из картона, сложить их в виде прямоугольника без отверстия, положить на лист бумаги и обвести карандашом по периметру. Складывая теперь части по-иному, можно видеть, что они по-прежнему не выходят за проведенную линию, хотя посредине прямоугольника образовалось отверстие.

К нашим двум частям можно, конечно, добавить третью, изготовленную в виде полосы, которая, будучи приложена к одной из сторон прямоугольника, превращает его в квадрат; таким образом мы получаем еще один способ разрезания квадрата на три части, дающий внутреннее отверстие.

Приведенные нами примеры ясно показывают, что область парадоксов с изменением площади еще только начинает разрабатываться. Существуют ли какие-нибудь криволинейные фигуры, например круги или эллипсы, которые можно разрезать на части, а затем составить по-иному так, чтобы при этом без заметного искажения фигуры получались внутренние отверстия?

Существуют ли трехмерные фигуры, специфичные именно для трех измерений, т. е. не являющиеся тривиальным следствием двумерных фигур? Ведь ясно, что к любой плоской фигуре, с которой мы встречались в этой главе, можно «добавить измерение», вырезая ее попросту из достаточно толстого картона, высота которого равна «длине третьего измерения» [24]).

Можно ли куб или, скажем, пирамиду разрезать не очень сложным способом на части так, чтобы, составляя их по-новому, получить заметные пустоты внутри?

Ответ будет таков: если не ограничивать число частей, то такие пространственные фигуры указать совсем нетрудно. Достаточно ясно это в случае куба.

Здесь внутренняя пустота может быть получена, однако вопрос о наименьшем числе частей, с которыми этого можно достигнуть, более сложен. Его заведомо можно изготовить из шести частей; не исключено, что этого можно добиться и с меньшим числом.

Такой куб можно эффектно демонстрировать следующим образом: вынуть его из ящичка, сделанного точно по кубу, разобрать на части, обнаружив при этом внутри шарик, снова сложить части в сплошной куб и показать, что он (без шарика) по-прежнему плотно заполняет ящик. Мы выскажем предположение, что должно существовать много таких фигур, как плоских, так и пространственных, к тому же отличающихся простотой и изяществом формы. Будущие исследователи этой любопытной области будут иметь удовольствие открыть их.

---

В этой главе мы рассмотрим головоломки с числами, для демонстрации которых не нужно никаких вспомогательных средств, за исключением карандаша и бумаги или, может быть, доски и куска мела.

Эти головоломки можно разбить на три основные категории:

а) головоломки, основанные на быстром счете;

б) головоломки с предсказанием результатов действий;

в) головоломки с отгадыванием чисел.

Существует обширная литература, посвященная первой из этих категорий. Однако быстрота вычислений в уме почти всегда демонстрируется как следствие совершенной техники счета, а не как фокус. Мы здесь лишь бегло коснемся четырех примеров быстрых вычислений, которые имеют большую популярность. Вот эти примеры:

1) нахождение дня недели, на который приходится какая-нибудь заданная дата;

2) ход шахматного коня;

3) построение волшебного квадрата по заданному числу (сумме);

4) быстрое извлечение кубического корня.

Демонстрация фокуса с извлечением кубического корня начинается с того, что кого-нибудь из присутствующих просят взять любое число от 1 до 100, возвести его в куб и сообщить вслух результат. После этого показывающий мгновенно называет кубический корень из названного числа.

Для того чтобы показывать этот фокус, нужно сначала выучить кубы чисел от 1 до 10:

При изучении этой таблицы обнаруживается, что все цифры, на которые оканчиваются кубы, различны, причем во всех случаях, за исключением 2 и 3, а также 7 й 8, последняя цифра куба совпадает с числом, возводимым в куб. В исключительных же случаях последняя цифра куба равна разности между 10 и числом, возводимым в куб.

Покажем, как это обстоятельство используется для быстрого извлечения кубического корня. Пусть зритель, возводя некоторое число в куб, получил, например, 250 047. Последняя цифра этого числа 7, из чего немедленно следует, что последней цифрой кубического корня должно быть 3. Первую цифру кубического корня находим следующим образом. Зачеркнем последние три цифры куба (независимо от количества его цифр) и рассмотрим цифры, стоящие впереди, — в нашем случае это 250. Число 250 располагается в таблице кубов между кубами шестерки и семерки.

Меньшая из этих цифр — в нашем случае 6 — и будет первой цифрой кубического корня. Поэтому правильным ответом будет 63.

Чтобы лучше уяснить суть дела, приведем еще один пример. Пусть названо число 19 683. Его последняя цифра 3 указывает, что последней цифрой кубического корня будет 7. Зачеркивая последние три цифры, получаем число 19, которое лежит между кубом двойки и кубом тройки. Меньшим из этих чисел будет 2, поэтому искомым кубическим корнем будет 27.

Может показаться странным, но для извлечения целочисленных корней из степеней более высоких, чем третья, существуют более простые правила. Особенно легко находить корни пятой степени, потому что любое число и его пятая степень всегда оканчиваются одной и той же цифрой.

Другой, несколько менее известный вычислительный фокус состоит в почти мгновенном сложении любых десяти последовательных чисел Фибоначчи (мы уже упоминали, что так называют ряд чисел, в котором каждое, начиная с третьего, представляет собой сумму двух предшествующих). Этот фокус демонстрируют так: показывающий просит кого-нибудь записать друг под другом два любых числа, какие он пожелает. Допустим для примера, что были выбраны 8 и 5.

Затем зритель должен сложить эти числа. Найденное таким образом третье число складывается со вторым (стоящим над ним), и получается четвертое число.

Этот процесс повторяют до тех пор, пока в вертикальном столбце не окажется десять чисел:

8

5

13

18

31

49

80

129

209

338

Во время записывания чисел показывающий стоит, повернувшись спиной к зрителям. Когда все числа будут записаны, он поворачивается, проводит под колонкой цифр черту и, не задумываясь, подписывает сумму этих чисел. Чтобы получить эту сумму, ему просто нужно взять четвертое число снизу и умножить его на 11 —операция, которую легко можно проделать в уме [25]). В нашем случае четвертым числом будет 80, поэтому в ответе получится число 80, взятое 11 раз, т. е. 880.

Фокусы с предсказанием результатов действий над числами и фокусы с отгадыванием чисел легко обратимы; под этим подразумевается, что фокус с предсказанием числа можно показывать как фокус с отгадыванием этого числа, и наоборот. Допустим, например, что показывающий знает наперед результат вычисления, который, как предполагает зритель, ему не может быть известен. Тогда показывающий может оформить фокус в виде предсказания, записав известный ему результат будущего вычисления на листке бумаги; в этом случае фокус следует рассматривать как фокус с предсказанием. Но этот же фокус он может оформить как «чтение мыслей» зрителя — после того как зритель закончит свои вычисления, — в этом случае фокус нужно отнести к категории фокусов с отгадыванием числа. (Третьим вариантом может быть оформление фокуса в виде молниеносного вычисления.) Большинству фокусов, о которых мы собираемся сейчас рассказать, можно придать любую из только что упомянутых форм; однако дальше мы не будем тратить понапрасну слов, останавливая на этом внимание зрителя.

Возможно, самый старинный из фокусов с предсказанием числа состоит в том, что кого-нибудь просят задумать число, проделать над ним ряд операций и затем объявить результат; после этого оказывается, что названное число совпадает с записанным в предсказании. На тривиальном примере фокус выглядит так: зрителя просят задумать число, затем удвоить его, прибавить к произведению 8, разделить полученное число пополам и, наконец, вычесть задуманное число. В ответе всегда будет половина того числа, которое вы велели прибавить. В нашем случае прибавлялось 8, поэтому в ответе будет 4. Если бы зрителю предложили прибавить 10, в ответе оказалось бы 5.

Более интересный фокус этого типа начинают с того, что зрителя просят записать год своего рождения и прибавить к нему год какого-нибудь выдающегося события в его жизни. К полученной сумме он должен будет добавить еще свой возраст и, наконец, число лет, прошедших с года знаменательного события. Только немногие сообразят, что сумма этих четырех чисел всегда будет равняться удвоенному числу, обозначающему текущий год [26]). Таким образом, вы, конечно, можете предсказать эту сумму наперед.

Этот фокус можно показывать и следующим образом. Когда зритель запишет год своего рождения, вы сообщаете ему, что благодаря передаче мыслей на расстояние это число стало вам известно, после чего записываете на своем листке произвольное число, не показывая его зрителю. Об остальных трех числах вы говорите, что они стали вам известны тем же путем. В действительности же вы пишете какие угодно числа! Пока зритель складывает свои четыре числа, вы делаете вид, что заняты тем же, причем в качестве суммы записываете число, которое, как вы знаете, должно служить суммой. Теперь вы говорите зрителю, что не хотите, чтобы присутствующие знали его возраст (если зритель принадлежит к слабому полу, такой оборот будет даже более естественным), и поэтому советуете ему зачернить карандашом все четыре слагаемых, оставив только сумму. Сами вы делаете то же самое! Теперь суммы сопоставляются и оказывается, что они одинаковы. Такой метод демонстрации создает впечатление, что вы как-то узнали все четыре числа, записанных зрителем, хотя, конечно, вы не знали ни одного из них. Заметим, что этот метод оказывается эффектным при показе любого числового фокуса с заранее известным ответом. Когда вы просите зрителя добавить свой возраст, не забудьте уточнить, что его нужно брать на 31 декабря текущего года. В противном случае его возраст в целых годах может оказаться на единицу меньше, чем разность между текущим годом и годом рождения, а тогда и вся его сумма будет меньше вашей на единицу. Можно предложить еще, чтобы зритель включал дополнительно в общую сумму какую-нибудь постороннюю цифру, например число людей, присутствующих в комнате.

Поскольку это число будет известно также и вам, для получения ответа нужно будет лишь добавить его к удвоенному текущему году. Таким образом, «пружинка» фокуса будет скрыта лучше. В случае, если вам придется повторять этот фокус, воспользуйтесь каким-нибудь другим числом (например, числом дней в текущем месяце), и ответы будут различными.

Вот один из самых замечательных фокусов этого рода. Его выделяет из подобных фокусов та особенность, что ни разу за все время демонстрации как при выполнении операций над задуманным числом, так и после получения окончательного результата зритель ничего не сообщает показывающему. И все же оказывается, что, пользуясь искусно созданными лазейками, можно постепенно подобраться к задуманному зрителем числу.

Демонстрацию фокуса можно разделить на следующие шаги:

1) Вы просите кого-нибудь задумать число от 1 до 10 включительно.

2) Велите умножить его на 3.

3) Предлагаете разделить полученное число на 2.

4) Теперь вам необходимо узнать, получилась ли у зрителя в частном смешанная дробь или целое число. Чтобы добыть нужные сведения, попросите его еще раз умножить результат на 3. Если это будет сделано быстро, без видимого напряжения, есть все основания быть уверенным, что зрителю не пришлось иметь дело с дробями. Если же у него получилась дробь, он запнется и, возможно, будет несколько удивлен. Он может даже спросить, как ему быть с дробной частью. В любом случае, если вам покажется, что у зрителя в частном получилась дробь, скажите примерно следующее: «Между прочим, ваш последний результат содержит дробную часть, неправда ли? Мне так почему-то показалось. Пожалуйста, округлите ваше число в большую сторону. Ну, например, если у вас получилось 10·1/2, возьмите вместо этого числа 11».

Теперь, если частное было дробным, запомните «ключевое число» 1. Если частное было целым, запоминать ничего не надо.

5) После того как в соответствии с предыдущей инструкцией было выполнено умножение на 3, велите зрителю снова разделить результат на 2.

6) Затем вам снова нужно знать, получилась ли в частном дробь или целое число. Вы говорите, например, следующее: «Теперь у вас в частном целое число, не так ли?». Если ответ будет утвердительным, произнесите: «Я так и думал» и переходите к дальнейшему. Если же вам ответят, что вы ошиблись, сделайте удивленное лицо и тут же скажите: «Ну, тогда освободитесь от дроби, взяв, как и в прошлый раз, ближайшее большее целое число».

В этом последнем случае запомните следующее ключевое число 2. Если же частное было целым, запоминать ничего не надо.

7) Предложите прибавить к результату 2.

Попросите вычесть 11. Конечно, два последних шага означают не что иное, как вычитание 9; однако эти ваши действия имеют целью замаскировать применение принципа девятки.

9) Если зритель объявит вам, что вычитание 11 произвести невозможно, потому что последнее полученное им число слишком мало, вы сразу же сможете назвать первоначально задуманное число. Так, например, если вам пришлось запоминать только ключевое число 1, была задумана единица; если вы запоминали ключевое число 2, была задумана двойка; если же приходилось запоминать оба ключевых числа — была задумана тройка (ее можно рассматривать как результат сложения обоих ключевых чисел); если же ничего не пришлось запоминать, была задумана четверка.

Допустим теперь, что вычитание числа 11 произвести можно, это будет означать, что задуманное число больше четырех.

Запомните ключевое число 4 и продолжайте следующим образом:

10) Попросите добавить к последнему результату 2.

11) Велите вычесть 11.

12) Если это сделать невозможно, тогда, сложив ключевые числа, вы получаете ответ. Если же зритель молча выполнил вычитание, сложите ключевые числа, прибавьте еще раз число 4 и вы получите задуманное число.

На первый взгляд этот фокус может показаться неоправданно сложным, но если вы его тщательно проработаете, вся процедура покажется вам совсем нетрудной. Конечно, вычитание девяток можно производить каким угодно способом. Например, вместо того чтобы прибавлять два и отнимать 11, можно предложить зрителю добавить 5 и вычесть 14 или прибавить 1 и вычесть 10. После нескольких демонстраций вы научитесь давать указания в такой форме, что у зрителя не будет возникать никаких подозрений, что своими ответами он дает нужную вам информацию о задуманном числе. После того как будет выполнена предложенная вами серия операций, кажущихся на первый взгляд бессмысленными и результаты которых к тому же не сообщаются, зритель с удивлением встретит объявление задуманного им числа [27]).

Секрет только что описанного фокуса основан на свойствах числа 9. Существует множество других фокусов с числами, в которых используются некоторые любопытные особенности числа 9. Например, написав в обратном порядке любое трехзначное число (при условии, что первая и последняя его цифры различны) и вычтя из большего числа меньшее, мы всегда получим в середине девятку и сумму крайних цифр, тоже равную 9. Это означает, что вы сразу можете назвать результат вычитания, зная только его первую или только последнюю цифру. Если теперь написать разность в обратном порядке и эти два числа сложить, то получится 1089. Один из популярных фокусов с числами состоит в следующем. Число 1089 пишется заранее на листке бумаги, который затем переворачивается лицевой стороной вниз. После того как зритель окончит серию операций, описанных выше, и объявит свой окончательный результат — 1089, покажите записанное вами предсказание, держа при этом лист вверх ногами. Написанное на нем число будет прочитано как 6801, что, конечно, не будет правильным ответом. Сделайте удивленное лицо, а затем извинитесь, что взяли лист не так, как нужно. Поверните его на 180° и покажите верное число. Это небольшое попутное представление вносит развлекательный момент в демонстрацию фокуса.

Если сложить все цифры некоторого числа, затем все цифры только что найденной суммы и так продолжать достаточно далеко, то получится одна единственная цифра, которая носит название цифрового корня первоначального числа. Быстрее всего можно получить цифровой корень при помощи так называемого «процесса отбрасывания девяток». Допустим, например, что мы хотим найти цифровой корень числа 87345691. Сначала сложим цифры 8 и 7, будет 15; затем тут же складываем 5 и 1, получаем 6. Этот же результат получится, если вычесть или «исключить» из 16 девятку. Теперь прибавим 6 к следующей цифре, т. е. к тройке, получится 9. Девять плюс 4 даст 13 — число, которое после исключения девятки опять сводится к числу 4. Так же мы поступаем, пока не дойдем до последней цифры. Цифра 7, полученная этим путем, будет цифровым корнем заданного числа 87345691.

Большое количество фокусов с числами основано на операции, которая приводит к числу, кажущемуся случайным, хотя в действительности имеющим своим цифровым корнем девятку. Если производилась именно такая операция, можно предложить зрителю обвести кружком любую цифру ответа (за исключением нуля), а остальные цифры назвать в любом порядке.

После этого показывающий может объявить отмеченную цифру. Для этого ему нужно просто складывать называемые зрителем цифры, вычитая по ходу дела девятки; таким образом, при объявлении последней цифры он уже будет знать цифровой корень совокупности записанных им чисел. Если этим корнем окажется девятка, то была отмечена кружком эта же цифра. В остальных случаях, чтобы получить отмеченную цифру, нужно вычесть найденный цифровой корень из девятки. Вот некоторые из многих операций, которые приводят к числам, цифровой корень которых равен 9.

1. Напишите число (оно может быть сколь угодно большим) и переставьте его цифры в любом порядке; вычтите меньшее из этих чисел из большего.

2. Напишите какое-нибудь число, сложите все его цифры и вычтите полученную сумму из первоначального числа.

3. Напишите какое-нибудь число. Найдите сумму его цифр, умножьте ее на 9 и сложите результат с первоначальным числом.

4. Напишите какое-нибудь число, умножьте его на 9 или на число, кратное девяти. (Все числа, кратные девяти, имеют своим цифровым корнем девятку, и обратно, все числа, имеющие своим цифровым корнем девятку, кратны девяти.)

5. Напишите какое-нибудь число, сложите два числа, полученных из него путем любой перестановки цифр, и возведите полученный результат в квадрат.

Если вы хотите еще более затемнить метод получения чисел, цифровой корень которых равен 9, вы можете перед существенным в этом методе действием вводить произвольные числа и операции. Например, можно предложить зрителю записать количество мелочи в его кармане, умножить это число на число людей в комнате, прибавить к результату самый знаменательный год в его жизни и т. д. и, наконец, умножить результат на 9. Ясно, что только последнее действие имеет отношение к делу. Как только получено число, цифровой корень которого равен 9, вы можете предложить зрителю обвести какую-нибудь цифру результата кружком и показывать фокус, как это было описано выше.

Возьмем какое-нибудь число, цифровой корень которого равен 9; образуем из него путем перестановки цифр второе число; переставляя снова цифры, получим третье число и будем так продолжать, пока не напишем столько чисел, сколько нам заблагорассудится. Сложив все эти числа, мы получим число, цифровой корень которого тоже будет равен девяти.

Аналогично, если число, имеющее своим цифровым корнем 9, умножить на целое число, то цифровой корень произведения будет равен 9.

Используя это свойство устойчивости корня относительно сложения и умножения, можно придумать много фокусов. Допустим, например, что у вас нашлась денежная бумажка, серийный номер которой имеет своим цифровым корнем девятку. Приберегите ее, пока вам не представится случай показать фокус. Попросите кого-нибудь написать несколько цифр наугад, затем, как бы вспомнив что-то, выньте денежную бумажку из кармана и предложите зрителю вместо этого лучше переписать ее серийный номер — удобный способ, поясняете вы, выбора произвольных чисел. Далее зритель несколько раз переставляет цифры, получая при этом все новые числа, складывает их, не показывая своих вычислений, умножает ответ на любое пришедшее ему в голову целое число и, наконец, обводит кружочком одну из цифр результата. После того как будут названы в любом порядке остальные цифры, вы сможете назвать ему отмеченное число.

Можно демонстрировать этот фокус и иначе, начав с чисел, входящих в дату демонстрации фокуса, т. е. порядкового номера месяца, дня месяца и года.

При записи года у вас будет выбор: либо брать две последние цифры, либо все четыре. Примерно два дня из каждых девяти (принадлежащих записи года) оказываются пригодными для образования числа, числовой корень которого равен девяти. В один из таких дней вы можете показать этот фокус. Допустим, что ваша дата 29 марта 1958 года. Попросите кого-нибудь записать ее в виде 29.3.58. Так как эта группа чисел имеет своим цифровым корнем девятку, вы можете продолжать далее, как в только что описанном фокусе с денежной бумажкой, или выбрать другую процедуру, не меняющую цифровой корень.

Интересный способ узнавания возраста некоторого лица начинается с того, что его просят выполнить ряд каких-нибудь действий, приводящих к числу, имеющему своим цифровым корнем девятку. Затем предлагают прибавить к полученному числу свой возраст и сообщить вам сумму. По этой сумме легко узнать возраст зрителя. Сначала найдите цифровой корень суммы. Затем прибавляйте к нему девятки до тех пор, пока полученное число не покажется вам наиболее близким к возрасту вашего собеседника. Это число и будет искомым возрастом. Допустим, например, что вы попросили зрителя написать любое число и умножить его на 9, после чего у него получилось 2826. К этому числу он добавил 40, свой возраст, и сообщил вам сумму: 2866. Цифровой корень этого числа равен 4; добавляя к четверке девятки, получим числа 13, 22, 31, 40, 49 и т. д., поскольку с точностью до 9 лет оценить возраст нетрудно, вы устанавливаете, что правильным ответом будет 40.

Бухгалтеры-ревизоры часто проверяют правильность сложения и умножения при помощицифровых корней. Например, сложение можно проконтролировать так: сначала найти цифровой корень всей совокупности цифр, входящих в слагаемые, а затем цифровой корень суммы. Если последняя была найдена правильно, корни должны совпасть. Это обстоятельство можно использовать для фокуса следующим образом.

Попросите кого-нибудь составить задачу на сложение, выписывая несколько многозначных чисел в столбик, одно под другим. Напрактиковавшись, вы сможете исключать девятки почти с такой же скоростью, с какой выписываются цифры, так что к концу составления задачи цифровой корень совокупности всех чисел будет вам известен. Затем вы поворачиваетесь спиной и просите произвести сложение. Если теперь зритель обведет кружком какую-нибудь цифру результата (не нуль), а остальные назовет в произвольном порядке, вы сможете объявить отмеченную цифру. Для этого нужно будет найти цифровой корень группы цифр, названных зрителем, а затем вычесть его из цифрового корня, найденного вначале (вы должны были его запомнить). Если второй корень окажется больше первого, добавьте перед вычитанием к первому корню девятку. Если корни окажутся одинаковыми, отмеченная цифра была, конечно, девяткой.

Подобный же фокус можно проделать, составив задачу на умножение; здесь мы будем опираться на тот факт, что цифровой корень произведения цифровых корней двух сомножителей равен цифровому корню произведения этих сомножителей. Итак, вы можете попросить кого-нибудь записать достаточно большое число, скажем, пяти- или шестизначное, и подписать под ним другое большое число. Следя за тем, как пишутся числа, вы определяете цифровые корни обоих сомножителей, перемножаете их и находите цифровой корень произведения.

Теперь вы поворачиваетесь спиной и предлагаете зрителю перемножить записанные им числа. Затем просите его обвести кружочком любую цифру результата (за исключением нуля) и назвать вслух остальные цифры в любом порядке. Как и в предыдущем фокусе, вы узнаете отмеченное число, вычитая цифровой корень совокупности названных зрителем цифр из цифрового корня, который вы должны были запомнить.

Если второй корень будет больше первого, опять-таки перед вычитанием добавьте к первому из них девятку.

Все «таинственные» свойства девятки объясняются тем простым фактом, что эта цифра является последней в употребляемой нами десятичной системе счисления. В восьмеричной системе счисления такими же любопытными свойствами обладает семерка. Это утверждение легко проверить. Прежде всего составим список шестнадцати чисел, обозначая их в восьмеричной системе, и выпишем рядом их эквиваленты в десятичной системе.

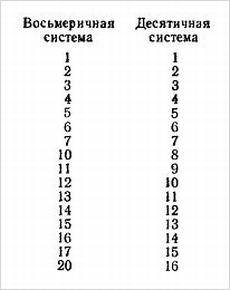
Предположим, что мы взяли число 341 (запись в восьмеричной системе) и вычли из него число 143, полученное обращением порядка записи цифр. Сначала отнимем 3 из 11. В десятичной системе это означало бы то же, что отнять 3 из 9. В ответе получилось бы 6. Но цифра 6 в обеих системах счисления обозначает одно и то же число, поэтому разность между 11 (запись в восьмеричной системе) и 3 равна 6. Продолжая далее вычитание этим же путем, получим в ответе 176 (запись в восьмеричной системе):

Вы замечаете, что цифрой, стоящей посередине, является семерка и что сумма крайних цифр тоже равна семи. Здесь происходит в точности то же самое, что и в варианте этого фокуса для десятичной системы, который мы описывали ранее, за исключением того, что ключевым числом является семерка, а не девятка.

Аналогичной проверке можно подвергнуть и все другие фокусы, основанные на свойствах девятки в десятичной системе. При этом для каждого из них найдется соответствующий фокус в восьмеричной системе, но роль «таинственного числа» будет принадлежать семерке. Выбирая соответствующую систему счислений, можно перенести особые свойства на любое желаемое число. Таким образом, становится очевидным, что эти свойства вытекают не из внутренних особенностей девятки, а только из того факта, что она является последней цифрой в нашей десятичной системе счисления.

Смешивание внутренних свойств числа с свойствами, вытекающими из его местоположения в данной системе счисления, является обычной ошибкой. Так, одно время думали, что по каким-то скрытым причинам среди цифр, изображающих бесконечную непериодическую десятичную дробь, обозначающую число я, семерка встречается в среднем реже других цифр. «Существует только одно число, настолько неравноправное среди других чисел, что невероятно, чтобы это могло быть случайностью, — писал доктор Огастес де Морган, — и это число есть таинственная семерка». Де Морган гчсал это, конечно, не всерьез; он хорошо знал, что цифры числа я в другой системе счисления будут совершенно отличными. В действительности даже в десятичной системе кажущейся редкость появления семерки в числе я объясняется ошибкой, допущенной Уильямом Шенксом при вычислении этого числа. В 1873 году, после пятнадцати лет упорного труда, Шенкс вычислил число π с семьсот семью десятичными знаками (ошибка, допущенная им на 528-м знаке, свела на нет все последующие вычисления). В 1949 году вычислительная машина ЭНИАК, так сказать, в виде отдыха от более сложных заданий вычислила π более чем с 2000 верными десятичными знаками. При этом никаких «таинственных» отклонений в частоте появления какой-нибудь цифры обнаружено не было [28]).

Можно ли знать наперед сумму, которая получится в результате сложения чисел, произвольно заданных присутствующими в аудитории? Фокусники придумали много остроумных решений этой задачи, которыми мы здесь не собираемся заниматься, так как они основаны на использовании подставных лиц, ловкости рук и других приемах нематематического характера.

Если же дать показывающему право называть слагаемые, чередуясь со зрителем, то он может получить желаемую сумму, не пользуясь при этом никакими нематематическими средствами. Самый простой и самый старый метод для этого следующий: допустим, что вы хотите получить в ответе 23 843. Отбросьте первую цифру, т. е. 2, а затем сложите ее с оставшимся числом, получится 3845. Это число вы напишите первым.

Теперь попросите зрителя подписать внизу любое четырехзначное число:

3 845

1528.

Под этими двумя числами вы пишете, как должно казаться зрителям — наугад, третье четырехзначное число. В действительности же под каждой цифрой, написанной зрителем, вы пишете ее дополнение до девятки:

3 845

1 528

8471.

Далее пишет свое второе четырехзначное число зритель. Третье число пишете вы, причем, как и в предыдущем случае, составляете его из цифр, дополняющих до девяток цифры зрителя.

Сумма выписанных пяти чисел в точности равна 23 843. В рассмотренном только что примере первая цифра предсказанного ответа была равной 2. Ей соответствовали две пары чисел, у которых сумма цифр, стоящих друг над другом, составляла 9, а всего слагаемых было пять. Если первой цифрой назначенной суммы будет цифра 3, то нужно брать три пары чисел с суммой стоящих друг над другом цифр, равной 9, и т. д. Во всех случаях первое число, которое нужно записать, вы получаете, отбрасывая первую цифру предсказанной суммы, а затем складывая ее с оставшимся числом. Фокус можно показывать с числами, составленными из любого числа цифр. Нужно только, чтобы во всех слагаемых оно было одинаковым.

Существует много вариантов этого фокуса. Например, первое число может написать зритель. Тогда ваше число, которое вы записываете под числом зрителя, нужно выбрать так, чтобы цифры, стоящие друг над другом, давали в сумме девятку. Далее зритель пишет третье число, вы пишете по тому же принципу четвертое число. Зритель пишет пятое и последнее число, после чего вы подводите черту и мгновенно подписываете сумму. Или, если вам это покажется более эффективным, пока зритель суммирует числа, поворачиваетесь спиной, а затем, не глядя на записанное, объявляете результат. Ответ получается, конечно, следующим образом: из последнего написанного числа нужно вычесть двойку и поставить ее перед полученным числом.

По желанию вы можете затянуть процесс суммирования. Например, можно вместе со зрителем записать шесть пар слагаемых, каждая из которых дает в сумме девятки. Последнее число, которое запишет зритель, доведет количество слагаемых до 13; чтобы получить теперь ответ, нужно из тринадцатого числа вычесть 6, а затем написать 6 перед числом, полученным в остатке. Если вообразить себе, что сложение распространится, скажем, на 28 пар чисел, прежде чем будет написано последнее число, принцип фокуса остается неизменным: вычтите 28 из последнего числа и поставьте 28 перед полученным остатком.

Существует еще один вариант фокуса, когда предсказание записывает зритель. Допустим, он выбрал число 538. Отбросьте пятерку и сложите ее с остатком, получится 43. Это число вы записываете первым.

Теперь поочередно со зрителем, пользуясь принципом девятки, вы записываете числа в столбик, пока под первым числом не окажется пять пар:

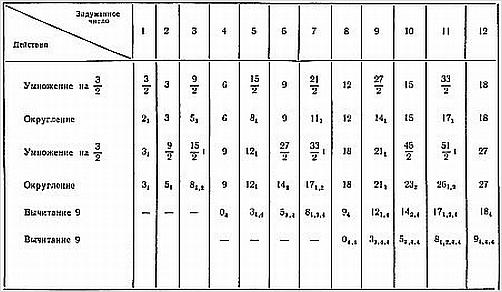
В ответе, конечно, получается число, предсказанное зрителем.

Еще одна категория фокусов с числами, совсем отличная от фокусов с предсказанием или отгадыванием числа, основана на том, что называют психологическими моментами. Эти фокусы не всегда получаются, но по каким-то неведомым причинам психологического характера шансы на успех при их демонстрации оказываются значительно большими, чем этого можно было ожидать. Вот простой пример. Если вы попросите назвать какое-нибудь число от 1 до 10, большинство людей назовет семерку, а если заданные границы будут 1 и 5, то — тройку.

Еще один любопытный психологический фактор, неизвестно кем впервые подмеченный, можно использовать в фокусе следующим образам. Напишите на клочке бумаги число 37 и отложите его в сторону. Затем, обращаясь к кому-нибудь из присутствующих, скажите: «Назовите, пожалуйста, двузначное число между 1 и 50, чтобы обе его цифры были нечетными и различными. Например, число 11 называть нельзя».

Может показаться странным, но много шансов, что зритель назовет 37 (второе наиболее вероятное число 35). В сущности, его выбор ограничен восемью числами, причем упоминание числа 11 как бы привлекает его мышление к числам третьего десятка.

Если этот фокус у вас получится, попробуйте за ним другой. На этот раз попросите назвать двузначное число между 50 и 100, обе цифры которого должны быть четными и, как и в предыдущем случае, различными. В данном случае выбор зрителя ограничен семью числами, из которых как будто чаще всех называют 68. Если под руками имеются игральные карты, можно предсказать это число, положив на стол шестерку и восьмерку лицевой стороной вниз. Это повышает ваши шансы на успех, так как вы имеете выбор между двумя возможными ответами, т. е. между 68 и 86, в зависимости от того, какую карту вы откроете первой.

---

1 Автор имеет в виду стандартную колоду из 52 карт, по 13 карт каждой масти, и использует следующую нумерацию карт в пределах данной масти:

1 — туз, 2 — двойка, 3 — тройка, 4 — четверка, 5 — пятерка, 6 — шестерка, 7 — семерка, 8 — восьмерка, 9 — девятка, 10 — десятка, 11 —валет, 12 — дама, 13 — король.

2 Предположим, что у зрителя имеется k карт, у показывающего N > k карт; пусть, далее, выбрано число m < N.

Очевидное равенство

N = k + m + (N — k — m)

является математическим эквивалентом утверждения, показывающего: «у меня имеется на m карт больше, чем у зрителя, и еще столько, чтобы от числа карт зрителя (k) досчитать до числа N — m».

Число m следует выбирать маленьким; если m + k будет больше, чем N, то разность N — k — m окажется отрицательной.
 
3 Истинная цель действий показывающего сводится к отсчету с помощью зрителя сорока карт, причем так, чтобы зритель не догадался об этом. Если x₁, х₂, х₃, x₄ — числовые значения взятых карт, то откладывается соответственно 10 — x₁, 10 — x₂, 10 — x₃, 10 — x₄ — карт; всего отложено 40 — x₁ — х₂ — x₃ — х₄ карт, следовательно, до 40 не хватает как раз х₁ + x₂ + x₃ + x₄ карт.

4 Девятая карта снизу является сорок четвертой сверху. Если совпадения не происходит, откладывается 11 карт.

Если совпадение происходит на карте с числовым значением n, то отсчитано, считая и ее, 11 — n карт; зритель затем отсчитывает n карт, что дает снова 11 карт. Четырехкратное повторение процедуры дает 44 карты, что и требуется.
 
5 «Снять» колоду означает: разделив колоду на две части, поменять их местами. Если карты колоды записать последовательно на окружности (образовать «цикл»), то операция «снятия», не меняя порядка карт в цикле, изменяет только начало отсчета.

6 При снятии восьми карточной колоды вида ABCDABCD вторая четверка карт всегда совпадает с первой.

7 Для любого числа между 10 и 19 разность между этим числом и суммой его цифр всегда равна 9, так что мы после указанных операций всегда попадаем на девятую карту.

8 Для любого числа между 20 и 29 разность между этим числом и суммой его цифр всегда равна 18. Чтобы фокус удался, нужно, чтобы часть колоды, «снятая» зрителем, насчитывала не менее 20 и не более 29 карт.

9 После ряда снятий расположение карт в тринадцатикарточной колоде с первоначальным расположением (верх) 13, 12, 11…. 3, 2, 1 (низ) заменится следующим: (верх) k — 1, k — 2…. 2, 1, 13, 12…. k (низ), где 1 <= k <= 13. Выше карты 13 лежит k — 1 карт, и сама карта 13 является k-й картой сверху.

Затем в результате перевода одной карты снизу колоды наверх на k-м месте сверху будет лежать карта 1, в результате перевода двух карт — карта 2 и т. д.; таким образом, если в результате снятия перенесено снизу вверх, положим, m карт, то на k-м месте сверху будет лежать карта m, что и требуется.
 
10 Пусть m < 26 и n > 26 — числа, названные зрителем. Если первоначальное расположение карт в колоде было (верх) 1, 2, 3…., m — 1, m, m + 1…. n — 1, n, 51, 52 (низ), то после первой процедуры оно становится следующим:

(верх) m — 1, m — 2…. 1; m, m + 1, n — 1, n…, 51, 52, (низ), а после второй процедуры — следующим: (верх) n — 1, n — 2…, m + 1, m, 1, 2…. m — 1; n…. 51, 52 (низ.) Очевидно, если отсчитать сверху n — m карт, следующей будет 1, что и требуется.

11 Потому что число костей, содержащих на одной из половинок заданное число очков, четно (если не принимать во внимание дубля), а внутри цепи такие кости расставлены парами.
 
12 Если m — наименьшее число в указанном квадрате, то весь квадрат имеет вид

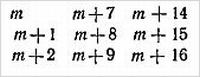
и сумма всех чисел квадрата равна 9m + 72 = 9(m + 8).

13 Сумма чисел, выбранных по одному из каждой строки и каждого столбца квадрата, равна сумме чисел на диагонали. Эта последняя есть сумма четырех членов арифметической прогрессии (с разностью и равна, в силу известной формулы, удвоенной сумме первого и последнего членов.

14 Если зритель задумал k, то до двенадцати остается 12 — k, или 20 — 8 — k, что и отсчитывается показывающим.

15 Два результата, которые нужно сложить, располагаются на циферблате симметрично относительно диаметра, проходящего через начало отсчета (указанное игральной костью).

Так как шкала часов равномерна, то сумма результатов равна удвоенному числу в начале отсчета, если заменить при этом 12 на нуль, 11 — на 1 и т. д., а это означает, что если результат больше 12, то из него нужно вычесть 12, а затем полученную разность разделить пополам.

16 Обозначим первоначальное число спичек через d. После первой операции в крайних кучках останется по d — 3 спичек, а в средней их станет d + 6. После второй операции, состоящей в переносе d — 3 спичек из средней кучки в крайнюю, в средней останется (d + 6) + (d — 3) = 9 спичек.

17 Тот же принцип, который был отмечен в примечании 16.

18 Математическая суть этого фокуса состоит в том факте, что сумма 2q + 3r + 5s получает шесть различных значений, когда q, r, s принимают значения 1, 2, 3 или какую-нибудь их перестановку.

Между прочим, коэффициенты 2, 3, 5 — не наименьшие из возможных в этом фокусе. Можно было бы использовать с тем же успехом, например, коэффициенты 1, 3, 4 (А совсем не берет спичек, Б берет дважды столько, сколько у него на руках, В — трижды столько); при этом все суммы не превосходят 19, т. е. можно ограничиться 19 спичками. 
 
19 Счет заканчивается на той монете, которая окажется последней, если ножку девятки монета за монетой накладывать на кольцо по часовой стрелке, начиная от монеты, следующей (по часовой стрелке) за той, к которой подходит ножка.

20 Общее число шашек, стоящих в четных вертикальных рядах, изменяется (в ту или иную сторону) ровно на 1 при каждом ходе. При четном числе ходов четность этого числа не изменится и останется такой же, как при первоначальном размещении шашек. Для размещения AAA это число нечетно, а для размещения ВВВ оно четно.

21 Ниже приводим 8 таких карточек:

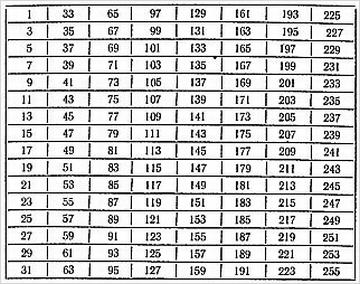
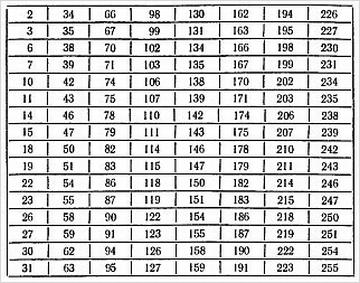
22 Можно предложить также следующую систему раскраски пластинок и нанесения чисел:
 

23 Сумма тонких цифр равна 15, а разность между жирной цифрой и тонкой на каждой фишке есть 5. Поэтому если в начале опыта было k фишек с жирными цифрами, то общая сумма всех цифр, открытых зрителям, была равна 15 + 5k. Допустим, что зритель перевернул i фишек с жирными цифрами и j — с тонкими. Показывающий просит перевернуть обратно эти i фишек и еще k — i фишек, остающихся с жирными цифрами, в итоге общая сумма будет

15 + 5k + 5j — 5(k — i) = 15 + 5(i + j) = 30,

причем число фишек с жирными цифрами оказывается равным i + j = 3. Пусть, далее, зритель переворачивает и закрывает р фишек с жирными и q с тонкими цифрами. В результате общая сумма цифр на шести фишках станет

30 — 5p + 5q = 30 — 5p + 5(3 — p) = 45–10p = 10(3 — p)+15,

что и дает схему вычислений автора.

Можно упростить счет, если не заставлять зрителя перевертывать накрываемые фишки; тогда сумма цифр накрытых фишек получится вычитанием из 30 суммы цифр открытых фишек.

24 То же требование о нетрнвнальности следует отнести и к проблеме о разрезании криволинейных плоских фигур. Ясно, что если разрезание и составление по-новому допускает квадрат, то допускает разрезание и составление также плоская фигура с любой границей, содержащая данный квадрат внутри себя.

25 Ряд, аналогичный ряду Фибоначчи, но начинающийся не с 1 и 1, а с любых чисел а и Ь, имеет вид

а, Ь, a + b, a +2b, 2a + 3b, За + 5b, 5а + 8b, 8a + 13b, 13a + 21b, 21a + 34b…

Его коэффициенты суть числа Фибоначчи, а сумма выписанных десяти членов равна, как легко сосчитать, 55a + 88b — на одно b меньше, чем второе из следующих за написанными чисел ряда.

26 Если N₀ — год рождения, N₁ — год выдающегося события, a N₂ — текущий год, то мы получает сразу

N₀ + N₁ + (N₂ — N₀) + (N₂ — N₁) = 2N₂,

что и требуется.
 
27 На стр. 123 приведена схема действий в этом фокусе.

Индексы 1, 2, 3, 4 означают ключевые числа, которые запоминает показывающий. Из схемы видно, что задуманное число есть сумма получающихся к концу процесса ключевых чисел. Интересно, что количество чисел, которые можно задумать, можно увеличить. Так, для числа 11 схема остается без изменения, для 12 придется еще раз вычесть 9, что даст третью четверку, и т. д.

28 Доказано, что частота появления любой цифры в десятичном разложении почти всех чисел одинакова и равна 1/10 (а в разложении с базой m равна — m/10). Числа, для которых это не выполняется, как говорят, образуют множество меры нуль, т. е, могут быть заключены в систему числовых промежутков с какой угодно малой общей длиной. См. статью А. Я. Хинчина в 1-м выпуске «Успехов математических наук» за 1936 год.